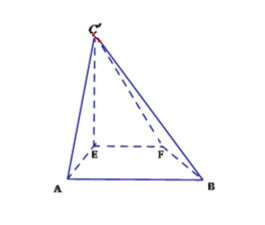
题目内容
【题目】已知椭圆![]() 的左、右焦点坐标为别为
的左、右焦点坐标为别为![]() ,
,![]() ,离心率是
,离心率是![]() . 椭圆
. 椭圆![]() 的左、右顶点分别记为
的左、右顶点分别记为![]() ,
,![]() .点
.点![]() 是椭圆
是椭圆![]() 上位于
上位于![]() 轴上方的动点,直线
轴上方的动点,直线![]() ,
,![]() 与直线
与直线![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)求线段![]() 长度的最小值.
长度的最小值.
(Ⅲ)当线段![]() 的长度最小时,在椭圆
的长度最小时,在椭圆![]() 上的点
上的点![]() 满足:
满足:![]() 的面积为
的面积为![]() .试确定点
.试确定点![]() 的个数.
的个数.
【答案】(1)![]() (2)
(2)![]() (3)2
(3)2
【解析】分析:(1)先根据焦点坐标得![]() ,再根据离心率得a,解得b,(2)设直线
,再根据离心率得a,解得b,(2)设直线![]() 的方程为
的方程为![]() ,解得S,得直线
,解得S,得直线![]() 的方程,与直线
的方程,与直线![]() 联立解得M,N坐标,即得
联立解得M,N坐标,即得![]() ,最后根据基本不等式求最值,(3)当线段
,最后根据基本不等式求最值,(3)当线段![]() 的长度最小时,求出S,由
的长度最小时,求出S,由![]() 的面积得点
的面积得点![]() 到直线
到直线![]() 的距离等于
的距离等于![]() ,与点T在椭圆上,联立方程组,根据解的个数确定点
,与点T在椭圆上,联立方程组,根据解的个数确定点![]() 的个数.
的个数.
详解:解:(Ⅰ)∵![]() ,且
,且![]() ,
,
∴![]() ,
,![]() ,
,
∴椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)易知椭圆![]() 的左、右顶点坐标为
的左、右顶点坐标为![]() ,
,![]() ,直线
,直线![]() 的斜率
的斜率![]() 显然存在,且
显然存在,且![]() ,故可设直线
,故可设直线![]() 的方程为
的方程为![]() ,
,
从而![]() .
.
由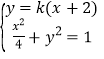 得
得![]() .
.
设![]() ,则
,则![]() ,得
,得![]() ,
,
从而![]() ,即
,即![]() .
.
又![]() ,故直线
,故直线![]() 的方程为
的方程为![]() ,
,
由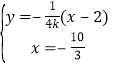 得
得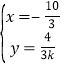 ,
,
∴![]() ,故
,故![]() ,
,
当且仅当![]() ,即
,即![]() 时等号成立.
时等号成立.
故当![]() 时,线段
时,线段![]() 的长度取最小值
的长度取最小值![]() .
.
(Ⅲ)由(Ⅱ)知,当线段![]() 的长度最小值时,
的长度最小值时,![]() ,
,
此时![]() 的方程为
的方程为![]() ,
,![]() ,
,
∴![]() ,
,
要使![]() 的面积为
的面积为![]() ,只需点
,只需点![]() 到直线
到直线![]() 的距离等于
的距离等于![]() ,
,
所以点![]() 在平行于
在平行于![]() 且与
且与![]() 距离等于
距离等于![]() 的直线
的直线![]() 上.
上.
设![]() ,则由
,则由![]() ,解得
,解得![]() 或
或![]() .
.
①当![]() 时,由
时,由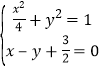 得
得![]() ,
,
∵![]() ,故直线
,故直线![]() 与椭圆
与椭圆![]() 有两个不同交点.
有两个不同交点.
②当![]() 时,由
时,由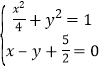 得
得![]() ,
,
∵![]() ,故直线
,故直线![]() 与椭圆
与椭圆![]() 没有交点.
没有交点.
综上所述,点![]() 的个数为
的个数为![]() .
.

练习册系列答案
相关题目