Question

【题目】如图所示，在四棱锥P－ABCD中，底面ABCD为平行四边形，∠ADC＝45°，AD＝AC＝1，O为AC的中点，PO⊥平面ABCD，PO＝2，M为PD的中点．

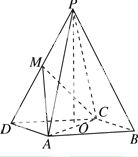
（1）证明：PB∥平面ACM；

（2）证明：AD⊥平面PAC．

Answer 1

【答案】（1）详见解析（2）详见解析

【解析】

试题（Ⅰ）证明PB∥平面ACM，利用线面平行的判定定理，证明MO∥PB即可；（Ⅱ）证明AD⊥平面PAC，利用线面垂直的判定定理，证明AD⊥AC，AD⊥PO即可；

试题解析：（1）连接BD，MO，在平行四边形ABCD中，因为O为AC的中点，所以O为BD的中点．又M为PD的中点，所以PB∥MO．因为PB平面ACM，MO平面ACM，所以PB∥平面ACM．

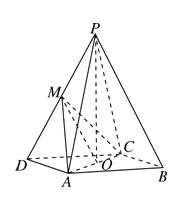
（2）因为∠ADC＝45°，且

AD＝AC＝1，

所以∠DAC＝90°，即AD⊥AC．又PO⊥平面ABCD，

AD平面ABCD，所以PO⊥AD．而AC∩PO＝O，所以AD⊥平面PAC．