题目内容
【题目】已知直线![]() :
:![]() ,半径为2的圆
,半径为2的圆![]() 与
与![]() 相切,圆心
相切,圆心![]() 在
在![]() 轴上且在直线
轴上且在直线![]() 的右上方.
的右上方.
(1)求圆的方程;
(2)若直线过点![]() 且与圆
且与圆![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 在
在![]() 轴上方,
轴上方,![]() 在
在![]() 轴下方),问在
轴下方),问在![]() 轴正半轴上是否存在定点
轴正半轴上是否存在定点![]() ,使得
,使得![]() 轴平分
轴平分![]() ?若存在,请求出点
?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() .
.
【解析】
试题分析:(1)设出圆心![]() 坐标,根据直线
坐标,根据直线![]() 与圆
与圆![]() 相切,得到圆心到直线
相切,得到圆心到直线![]() 的距离
的距离![]() ,确定出圆心
,确定出圆心![]() 坐标,即可得出圆
坐标,即可得出圆![]() 方程;(2)当直线
方程;(2)当直线![]() 轴,则
轴,则![]() 轴平分
轴平分![]() ,当直线
,当直线![]() 斜率存在时,设直线
斜率存在时,设直线![]() 方程为
方程为![]() ,联立圆与直线方程,消去
,联立圆与直线方程,消去![]() 得到关于
得到关于![]() 的一元二次方程,利用韦达定理表示出两根之和与两根之积,由若
的一元二次方程,利用韦达定理表示出两根之和与两根之积,由若![]() 轴平分
轴平分![]() ,则
,则![]() ,求出
,求出![]() 的值,确定出此时
的值,确定出此时![]() 坐标即可.
坐标即可.
试题解析:
(1)设圆心![]() (
(![]() ),则
),则![]() ,解得
,解得![]() 或
或![]() (舍),所以圆
(舍),所以圆![]() :
:![]() .
.
(2)当直线![]() 轴时,
轴时,![]() 轴平分
轴平分![]() ,当直线
,当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
![]() ,
,![]()
![]() ,
,![]() ,
,
由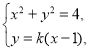 得
得![]() ,
,
∴![]() ,
,![]() ,
,
若![]() 轴平分
轴平分![]() ,则
,则![]() ,即
,即![]() ,
,
所以![]() ,即
,即![]() ,
,
![]() ,解得
,解得![]() ,
,
所以当点![]() 时,能使得
时,能使得![]() 总成立.
总成立.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】随机询问某大学40名不同性别的大学生在购买食物时是否读营养说明,得到如下列联表:
性别与读营养说明列联表:
男 | 女 | 总计 | |
读营养说明 | 16 | 8 | 24 |
不读营养说明 | 4 | 12 | 16 |
总计 | 20 | 20 | 40 |
(Ⅰ)根据以上列联表进行独立性检验,能否在犯错误的概率不超过0.01的前提下认为性别与是否读营养说明之间有关系?
(Ⅱ)从被询问的16名不读营养说明的大学生中,随机抽取2名学生,求抽到男生人数![]() 的分布列及其均值(即数学期望).
的分布列及其均值(即数学期望).
(注:![]() ,其中
,其中![]() 为样本容量.)
为样本容量.)