题目内容
在直角坐标系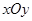 中,动点
中,动点 与定点
与定点 的距离和它到定直线
的距离和它到定直线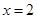 的距离之比是
的距离之比是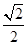 ,设动点
,设动点 的轨迹为
的轨迹为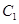 ,
,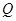 是动圆
是动圆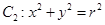
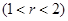 上一点.
上一点.
(1)求动点 的轨迹
的轨迹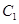 的方程;
的方程;
(2)设曲线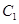 上的三点
上的三点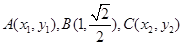 与点
与点 的距离成等差数列,若线段
的距离成等差数列,若线段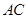 的垂直平分线与
的垂直平分线与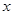 轴的交点为
轴的交点为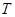 ,求直线
,求直线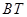 的斜率
的斜率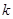 ;
;
(3)若直线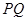 与
与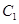 和动圆
和动圆 均只有一个公共点,求
均只有一个公共点,求 、
、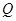 两点的距离
两点的距离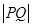 的最大值.
的最大值.
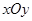 中,动点
中,动点 与定点
与定点 的距离和它到定直线
的距离和它到定直线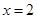 的距离之比是
的距离之比是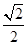 ,设动点
,设动点 的轨迹为
的轨迹为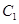 ,
,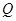 是动圆
是动圆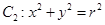
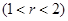 上一点.
上一点.(1)求动点
 的轨迹
的轨迹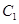 的方程;
的方程;(2)设曲线
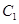 上的三点
上的三点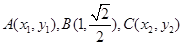 与点
与点 的距离成等差数列,若线段
的距离成等差数列,若线段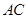 的垂直平分线与
的垂直平分线与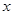 轴的交点为
轴的交点为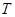 ,求直线
,求直线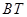 的斜率
的斜率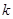 ;
;(3)若直线
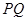 与
与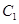 和动圆
和动圆 均只有一个公共点,求
均只有一个公共点,求 、
、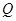 两点的距离
两点的距离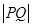 的最大值.
的最大值.(1)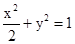 ;(2)
;(2)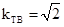 ;(3)
;(3)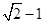 .
.
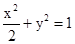 ;(2)
;(2)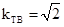 ;(3)
;(3)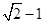 .
.本试题主要考查了轨迹方程的求解和椭圆的定义,以及直线与椭圆的位置关系的综合运用。
解:(1)由已知,得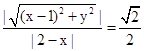 ,…………………………1分.
,…………………………1分.
将两边平方,并化简得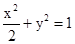 , …………………………3分.
, …………………………3分.
故轨迹C1的方程是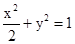 。 ………………4分.
。 ………………4分.
(2)由已知可得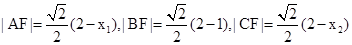 ,,,
,,,
因为2|BF|=|AF|=|CF|,所以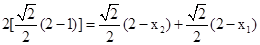
即得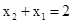 , ① …………………………5分.
, ① …………………………5分.
故线段AC的中点为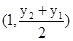 ,其垂直平分线方程为
,其垂直平分线方程为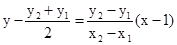 , ②
, ②
…………………………6分.
因为A,C在椭圆上,故有 ,
,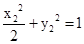 ,两式相减,
,两式相减,
得: ③
③
将①代入③,化简得 , ④ ………………………7分.
, ④ ………………………7分.
将④代入②,并令y=0得,x=1/2,即T的坐标为(1/2,0)。………………………8分.
所以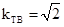 . ………………………9分.
. ………………………9分.
设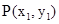 、
、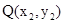 ,直线
,直线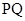 的方程为
的方程为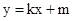
因为P既在椭圆C1上又在直线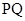 上,从而有
上,从而有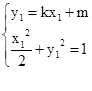
将(1)代入(2)得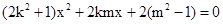 ………10分.
………10分.
由于直线PQ与椭圆C1相切,故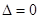
从而可得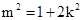 ,
,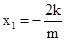 (3)
(3)
同理,由Q既在圆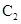 上又在直线
上又在直线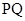 上,可得
上,可得
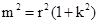 ,
,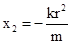 (4)……………………12分
(4)……………………12分
由(3)、(4)得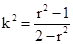 ,
,
所以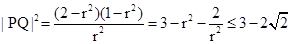 ……………………13分.
……………………13分.
即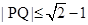 ,当且仅当
,当且仅当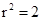 时取等号,
时取等号,
故P,Q、两点的距离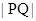 的最大值
的最大值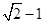 . …………………………14分.
. …………………………14分.
解:(1)由已知,得
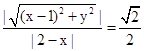 ,…………………………1分.
,…………………………1分.将两边平方,并化简得
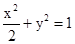 , …………………………3分.
, …………………………3分.故轨迹C1的方程是
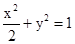 。 ………………4分.
。 ………………4分.(2)由已知可得
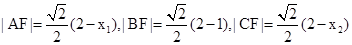 ,,,
,,,因为2|BF|=|AF|=|CF|,所以
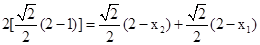
即得
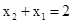 , ① …………………………5分.
, ① …………………………5分.故线段AC的中点为
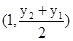 ,其垂直平分线方程为
,其垂直平分线方程为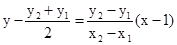 , ②
, ②…………………………6分.
因为A,C在椭圆上,故有
 ,
,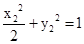 ,两式相减,
,两式相减,得:
 ③
③将①代入③,化简得
 , ④ ………………………7分.
, ④ ………………………7分.将④代入②,并令y=0得,x=1/2,即T的坐标为(1/2,0)。………………………8分.
所以
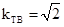 . ………………………9分.
. ………………………9分.设
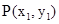 、
、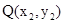 ,直线
,直线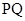 的方程为
的方程为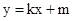
因为P既在椭圆C1上又在直线
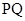 上,从而有
上,从而有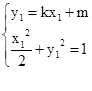
将(1)代入(2)得
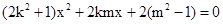 ………10分.
………10分.由于直线PQ与椭圆C1相切,故
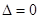
从而可得
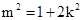 ,
,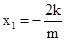 (3)
(3)同理,由Q既在圆
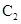 上又在直线
上又在直线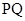 上,可得
上,可得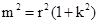 ,
,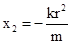 (4)……………………12分
(4)……………………12分由(3)、(4)得
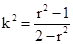 ,
, 所以
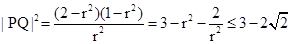 ……………………13分.
……………………13分.即
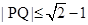 ,当且仅当
,当且仅当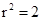 时取等号,
时取等号,故P,Q、两点的距离
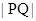 的最大值
的最大值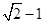 . …………………………14分.
. …………………………14分.
练习册系列答案
相关题目
 ;
;

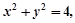 则
则 的最大值是_____________。
的最大值是_____________。 (
( ),过点
),过点 作抛物线
作抛物线 的切线,切点分别为
的切线,切点分别为 、
、 (其中
(其中 ).
).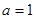 ,求
,求 与
与 的值;
的值; 与直线
与直线 相切,求圆
相切,求圆 ,且以点
,且以点 过圆
过圆 的圆心,则a的值为
的圆心,则a的值为 1
1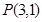 及两条直线
及两条直线 ,则过点
,则过点 且与两直线都相切的圆的方程是____________________________________________。
且与两直线都相切的圆的方程是____________________________________________。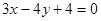 与圆C相切.
与圆C相切.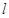 与圆C交于不同的两点A
与圆C交于不同的两点A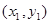 、B
、B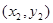 ,当
,当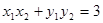 时,求△AOB的面积.
时,求△AOB的面积. 表示圆,则
表示圆,则 的取值 范围是( )
的取值 范围是( )


 轴相切的圆的方程是
轴相切的圆的方程是


