题目内容
已知等差数列 的公差大于0,且
的公差大于0,且 是方程
是方程 的两根,数列
的两根,数列 的前n项的和为
的前n项的和为 ,且
,且 (
( ).
).
(1) 求数列 ,
, 的通项公式;
的通项公式;
(2) 记 ,求证:
,求证: .
.
(1)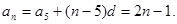

(2)利用数列的单调性,结合定义法作差法来得到单调性的证明。
解析试题分析:解:(Ⅰ)∵ 是方程
是方程 的两根,且数列
的两根,且数列 的公差
的公差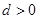 ,
,
∴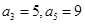 ,公差
,公差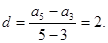
∴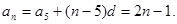 (
(  ) 4分
) 4分
又当n=1时,有b1=S1=1-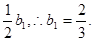
当
∴数列{bn}是等比数列,
∴ (
(  ) 8分
) 8分
(Ⅱ)由(Ⅰ)知 10分
10分
∴
∴ 12分
12分
考点:数列的通项公式
点评:解决的关键是能利用等差数列的概念和等比数列的通项公式来求解,属于基础题。

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
 的前四项和为10,且
的前四项和为10,且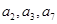 成等比数列
成等比数列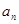
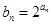 ,求数列
,求数列 的前
的前 项和
项和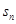
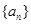 是等差数列,其中
是等差数列,其中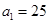 ,
,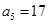 。
。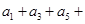 …
…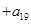 的值。
的值。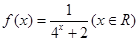 .
.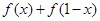 的值;
的值;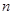 项和公式的推导方法,求:
项和公式的推导方法,求: 的值.
的值. 的前
的前 项和
项和 ,求证:
,求证:
 ,求
,求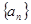 中,
中,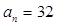 ,
, ,
, 为公差为11的等差数列,求
为公差为11的等差数列,求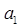 ;
;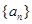 是以
是以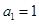 为首项、公比为
为首项、公比为 的等比数列,求
的等比数列,求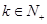 总有:
总有: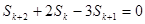
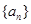 的各项均为正数,
的各项均为正数,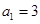 ,前
,前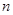 项和为
项和为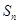 ,
,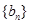 为等比数列,
为等比数列, 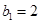 ,且
,且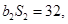
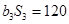 .
.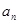 与
与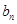 ;
;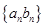 的前
的前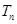 。
。 的前
的前 项和为
项和为 ,且
,且 ;数列
;数列 为等差数列,且
为等差数列,且 。
。 求证:数列
求证:数列 若
若 ,
, 为数列
为数列 的前
的前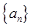 的公差
的公差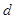 =1,前
=1,前 项和为
项和为 .
.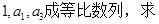
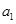 ;
;