题目内容
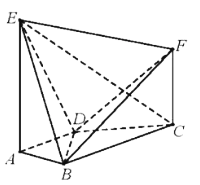
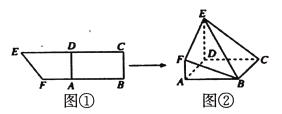
【题目】如图所示,在直角梯形BCEF中,∠CBF=∠BCE=90°,A,D分别是BF,CE上的点,AD∥BC,且AB=DE=2BC=2AF(如图1),将四边形ADEF沿AD折起,连结BE、BF、CE(如图2).在折起的过程中,下列说法中正确的个数( )
①AC∥平面BEF;
②B、C、E、F四点可能共面;
③若EF⊥CF,则平面ADEF⊥平面ABCD;
④平面BCE与平面BEF可能垂直
A.0B.1C.2D.3
【答案】C
【解析】
根据折叠前后线段、角的变化情况,由线面平行、面面垂直的判定定理和性质定理对各命题进行判断,即可得出答案.
对①,在图②中,连接![]() 交于点
交于点![]() ,取
,取![]() 中点,连接MO,易证AOMF为平行四边形,即AC//FM,所以AC//平面BEF,故①正确;
中点,连接MO,易证AOMF为平行四边形,即AC//FM,所以AC//平面BEF,故①正确;
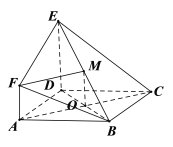
对②,如果B、C、E、F四点共面,则由BC//平面ADEF,可得BC//EF,又AD//BC,所以AD//EF,这样四边形ADEF为平行四边形,与已知矛盾,故②不正确;
对③,在梯形ADEF中,由平面几何知识易得EF![]() FD,又EF
FD,又EF![]() CF,∴EF
CF,∴EF![]() 平面CDF,
平面CDF,
即有CD![]() EF,∴CD
EF,∴CD![]() 平面ADEF,则平面ADEF
平面ADEF,则平面ADEF![]() 平面ABCD,故③正确;
平面ABCD,故③正确;
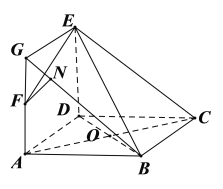
对④,在图②中,延长AF至G,使得AF=FG,连接BG,EG,易得平面BCE![]() 平面ABF,BCEG四点共面.过F作FN
平面ABF,BCEG四点共面.过F作FN![]() BG于N,则FN
BG于N,则FN![]() 平面BCE,若平面BCE
平面BCE,若平面BCE![]() 平面BEF,
平面BEF,
则过F作直线与平面BCE垂直,其垂足在BE上,矛盾,故④错误.
故选:C.

练习册系列答案
相关题目