题目内容
已知函数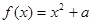 .
.
(1)若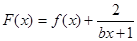 是偶函数,在定义域上
是偶函数,在定义域上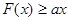 恒成立,求实数
恒成立,求实数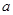 的取值范围;
的取值范围;
(2)当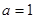 时,令
时,令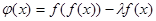 ,问是否存在实数
,问是否存在实数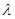 ,使
,使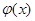 在
在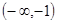 上是减函数,在
上是减函数,在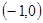 上是增函数?如果存在,求出
上是增函数?如果存在,求出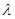 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
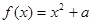 .
.(1)若
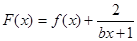 是偶函数,在定义域上
是偶函数,在定义域上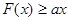 恒成立,求实数
恒成立,求实数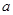 的取值范围;
的取值范围;(2)当
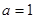 时,令
时,令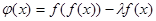 ,问是否存在实数
,问是否存在实数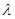 ,使
,使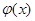 在
在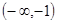 上是减函数,在
上是减函数,在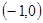 上是增函数?如果存在,求出
上是增函数?如果存在,求出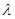 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.(1) 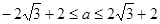
(2)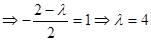
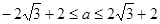
(2)
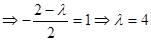
试题分析:解:(1)
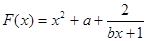 是偶函数,
是偶函数,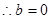 即
即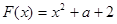 ,
, 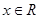
又
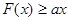 恒成立即
恒成立即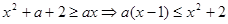
当
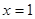 时
时
当
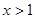 时,
时,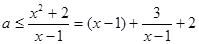 ,
,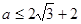
当
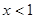 时,
时,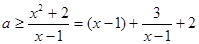 ,
, 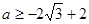
综上:
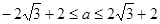
(2)
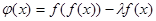
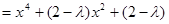
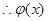 是偶函数,要使
是偶函数,要使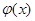 在
在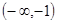 上是减函数在
上是减函数在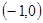 上是增函数,即
上是增函数,即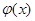 只要满足在区间
只要满足在区间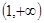 上是增函数在
上是增函数在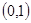 上是减函数 .
上是减函数 . 令
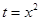 ,当
,当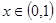 时
时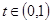 ;
;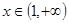 时
时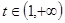 ,由于
,由于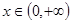 时,
时,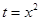 是增函数记
是增函数记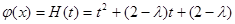 ,故
,故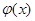 与
与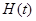 在区间
在区间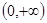 上有相同的增减性,当二次函数
上有相同的增减性,当二次函数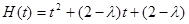 在区间
在区间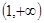 上是增函数在
上是增函数在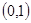 上是减函数,其对称轴方程为
上是减函数,其对称轴方程为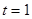
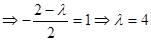 .
. 点评:主要是考查了函数奇偶性和单调性以及不等式的恒成立问题的综合运用,属于基础题。

练习册系列答案
相关题目
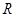 上的函数
上的函数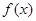 满足:
满足: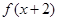 是偶函数,且
是偶函数,且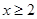 时的解析式为
时的解析式为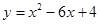 ,则
,则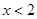 时
时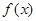 的解析式为 ;
的解析式为 ;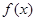 是定义在
是定义在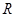 上的奇函数.当
上的奇函数.当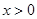 时,
时,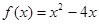 ,则不等式
,则不等式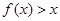 的解集用区间表示为 .
的解集用区间表示为 .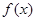 为奇函数,当
为奇函数,当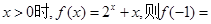 __________
__________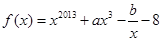 ,
,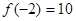 ,则
,则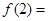 。
。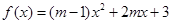 为偶函数,则m=
为偶函数,则m= 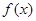
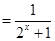
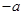 为奇函数,则
为奇函数,则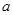 =
= 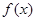 在R上的任一取值都有导数,且
在R上的任一取值都有导数,且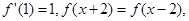 则曲线
则曲线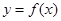 在
在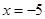 处的切线的斜率为 ( )
处的切线的斜率为 ( )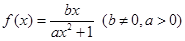 .
. 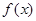 的奇偶性;
的奇偶性;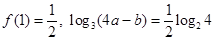 ,求
,求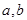 的值.
的值.