题目内容
袋中有大小相同的5个球，其中黑球3个，白球2个，甲乙二人分别从中各取一个，甲先取（不放回）乙后取。规定：
两人取到同颜色的球，由甲胜，取到不同颜色的球，则乙胜。
（1）分别求甲乙取到黑球的概率；
（2）甲乙二人谁胜的概率大，请说明理由。
两人取到同颜色的球，由甲胜，取到不同颜色的球，则乙胜。（1）分别求甲乙取到黑球的概率；
（2）甲乙二人谁胜的概率大，请说明理由。
（1）
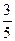
（2）乙胜出的概率大，因为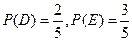
，
。
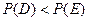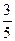
（2）乙胜出的概率大，因为
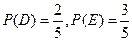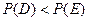，。（1）记“甲取到黑球”为事件A，“乙取到黑球为事件B”
则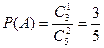
…………3分
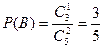
故甲、乙取到黑球的概率均为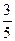。 …………6分
（2）记“两人取到同色球”为事件D，“两人取到异色的球”记为事件E
则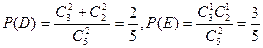
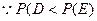
乙胜出的概率大。 …………12分
则
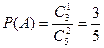…………3分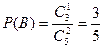 故甲、乙取到黑球的概率均为
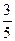。 …………6分（2）记“两人取到同色球”为事件D，“两人取到异色的球”记为事件E
则
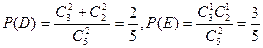
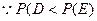
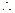乙胜出的概率大。 …………12分
练习册系列答案
相关题目
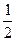，且面试是否合格互不影响。求：
，回答第三题正确的概率为
，且各题回答正确与否相互之间没有影响．记这位挑战者回答这三个问题的总得分为
。
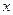和该年支出维修费用
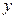（万元），得到数据如下：
）
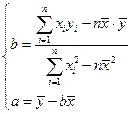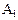=“第i次抽到红球”，（
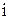="1," 2, 3）。试用
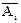表示下列事件：