题目内容
利用随机模拟方法计算图3-3-14中阴影部分(y=x3和x=2以及x轴所围成的部分)的面积.
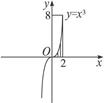
图3-3-14

图3-3-14
(1)利用计算器或计算机产生两组0至1区间的均匀随机数,a1=RAND,b1=RAND;
(2)进行伸缩变换,a=a1*2,b=b1*8;
(3)数出落在阴影内(满足b<a3)的样本点数N1,用几何概型公式计算阴影部分的面积.
例如做1 000次试验,即N="1" 000,模拟得到
N1=250.
由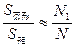 ,得S阴影≈
,得S阴影≈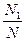 ×S矩=
×S矩=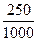 ×16=4.
×16=4.
(2)进行伸缩变换,a=a1*2,b=b1*8;
(3)数出落在阴影内(满足b<a3)的样本点数N1,用几何概型公式计算阴影部分的面积.
例如做1 000次试验,即N="1" 000,模拟得到
N1=250.
由
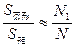 ,得S阴影≈
,得S阴影≈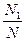 ×S矩=
×S矩=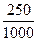 ×16=4.
×16=4.在坐标系中画出矩形(x=0,x=2,y=0,y=8所围成的部分),利用面积比与概率、频率的关系进行;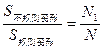 ,应当作公式记住,当然应理解其来历,其中N为总的试验次数,N1为落在不规则图形内的试验次数.
,应当作公式记住,当然应理解其来历,其中N为总的试验次数,N1为落在不规则图形内的试验次数.
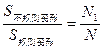 ,应当作公式记住,当然应理解其来历,其中N为总的试验次数,N1为落在不规则图形内的试验次数.
,应当作公式记住,当然应理解其来历,其中N为总的试验次数,N1为落在不规则图形内的试验次数.
练习册系列答案
相关题目
 道备选题中一次性随机抽取
道备选题中一次性随机抽取 题,按照题目要求独立完成全部实验操作. 规定:至少正确完成其中
题,按照题目要求独立完成全部实验操作. 规定:至少正确完成其中 题的便可通过考查. 已知
题的便可通过考查. 已知 题能正确完成,
题能正确完成, ,且每题正确完成与否互不影响. 求:
,且每题正确完成与否互不影响. 求:

 ,其中
,其中 ,
, ;参考数据:
;参考数据: ,
, ,
, ,
, ,
, ,
, ,
, )
) 两人取到同颜色的球,由甲胜,取到不同颜色的球,则乙胜。
两人取到同颜色的球,由甲胜,取到不同颜色的球,则乙胜。 、
、 、
、 ,且各道工序互不影响。
,且各道工序互不影响。
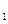

 的分布列,并求
的分布列,并求