题目内容
【题目】某科研团队研发了一款快速检测某种疾病的试剂盒.为了解该试剂盒检测的准确性,质检部门从某地区(人数众多)随机选取了![]() 位患者和
位患者和![]() 位非患者,用该试剂盒分别对他们进行检测,结果如下:
位非患者,用该试剂盒分别对他们进行检测,结果如下:
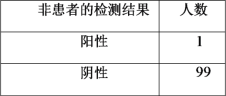
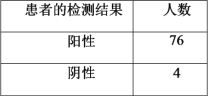
(1)从该地区患者中随机选取一人,对其检测一次,估计此患者检测结果为阳性的概率;
(2)从该地区患者中随机选取![]() 人,各检测一次,假设每位患者的检测结果相互独立,以
人,各检测一次,假设每位患者的检测结果相互独立,以![]() 表示检测结果为阳性的患者人数,利用(1)中所得概率,求
表示检测结果为阳性的患者人数,利用(1)中所得概率,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)假设该地区有![]() 万人,患病率为
万人,患病率为![]() .从该地区随机选取一人,用该试剂盒对其检测一次.若检测结果为阳性,能否判断此人患该疾病的概率超过
.从该地区随机选取一人,用该试剂盒对其检测一次.若检测结果为阳性,能否判断此人患该疾病的概率超过![]() ?并说明理由.
?并说明理由.
【答案】(1)![]() (2)详见解析(3)此人患该疾病的概率未超过
(2)详见解析(3)此人患该疾病的概率未超过![]() ,理由见解析
,理由见解析
【解析】
(1)直接用古典概型的概率公式计算可得答案;
(2)可知随机变量![]() 服从二项分布,即
服从二项分布,即![]() ,其中
,其中![]() ,
,![]() ,根据二项分布的概率公式可得分布列和数学期望;
,根据二项分布的概率公式可得分布列和数学期望;
(3)根据患病率为![]() 可知10万人中由99000人没患病,1000人患病,没患病检测呈阳性的有990人,患病的检测呈阳性的950人,共有990+950=1450人呈阳性,所其中只有950人患病,所以患病率为
可知10万人中由99000人没患病,1000人患病,没患病检测呈阳性的有990人,患病的检测呈阳性的950人,共有990+950=1450人呈阳性,所其中只有950人患病,所以患病率为![]() ,由此可得答案.
,由此可得答案.
(1)由题意知,![]() 位患者中有
位患者中有![]() 位用该试剂盒检测一次,结果为阳性.
位用该试剂盒检测一次,结果为阳性.
所以从该地区患者中随机选取一位,用该试剂盒检测一次,结果为阳性的概率估计为![]() .
.
(2)由题意可知![]() ,其中
,其中![]() ,
,![]() .
.
![]() 的所有可能的取值为
的所有可能的取值为![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
所以![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
|
|
故![]() 的数学期望
的数学期望![]() .
.
(3)此人患该疾病的概率未超过![]() .理由如下:
.理由如下:
由题意得,如果该地区所有人用该试剂盒检测一次,那么结果为阳性的人数为
![]() ,其中患者人数为
,其中患者人数为![]() .
.
若某人检测结果为阳性,那么他患该疾病的概率为![]() .
.
所以此人患该疾病的概率未超过![]() .
.

 名校课堂系列答案
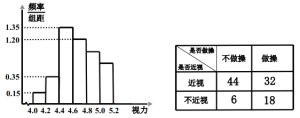
名校课堂系列答案【题目】眼保健操是一种眼睛的保健体操,主要是通过按摩眼部穴位,调整眼及头部的血液循环,调节肌肉,改善眼的疲劳,达到预防近视等眼部疾病的目的.某学校为了调查推广眼保健操对改善学生视力的效果,在应届高三的全体800名学生中随机抽取了100名学生进行视力检查,并得到如图的频率分布直方图.
(1)若直方图中后三组的频数成等差数列,试估计全年级视力在5.0以上的人数;
(2)为了研究学生的视力与眼保健操是否有关系,对年级不做眼保健操和坚持做眼保健操的学生进行了调查,得到下表中数据,根据表中的数据,能否在犯错的概率不超过0.005的前提下认为视力与眼保健操有关系?
(3)在(2)中调查的100名学生中,按照分层抽样在不近视的学生中抽取8人,进一步调查他们良好的护眼习惯,在这8人中任取2人,记坚持做眼保健操的学生人数为X,求X的分布列和数学期望.
附: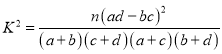
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |