题目内容
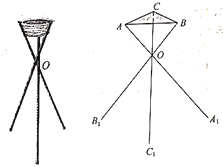
【题目】在四棱锥P-ABCD，四边形ABCD是边长为3的正方形，平面
平面
，
于点O，
，点E在棱PB上，
.
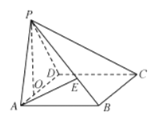
（1）当
时，求直线AE与平面PCD所成角的正弦值；
（2）若二面角B-PC-D的余弦值为
，求PO的长.
【答案】（1）
；（2）1.
【解析】
（1）先证明
平面
，然后以OP为z轴，建立空间直角坐标系Oxyz，算出
和平面PCD的法向量的坐标即可
（2）设
，分别算出平面PCD和平面BPC的法向量即可.
（1）
平面
平面，
，平面
平面
平面
平面.
以OP为z轴，建立空间直角坐标系Oxyz，
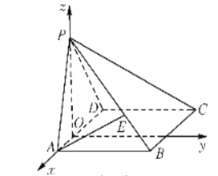
则
，
，
，
，
，
，
，
.
设平面PCD的法向量
，
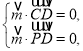即
取
.
设直线AE与平面PCD所成角为
，则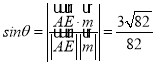
，
直线AE与平面PCD所成角的正弦值为.
（2）设，则
，
，
，
，.
设平面PCD法向量
，则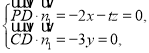
取
，同理可得平面BPC法向量
，
.
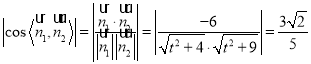，解得
.
当二面角B─PC─D的余弦值为
时，
.
【题目】在抗击新冠肺炎疫情期间，很多人积极参与了疫情防控的志愿者活动.各社区志愿者服务类型有：现场值班值守，社区消毒，远程教育宣传，心理咨询（每个志愿者仅参与一类服务）.参与A，B，C三个社区的志愿者服务情况如下表：
社区 | 社区服务总人数 | 服务类型 | |||
现场值班值守 | 社区消毒 | 远程教育宣传 | 心理咨询 | ||
A | 100 | 30 | 30 | 20 | 20 |
B | 120 | 40 | 35 | 20 | 25 |
C | 150 | 50 | 40 | 30 | 30 |
（1）从上表三个社区的志愿者中任取1人，求此人来自于A社区，并且参与社区消毒工作的概率；
（2）从上表三个社区的志愿者中各任取1人调查情况，以X表示负责现场值班值守的人数，求X的分布列；
（3）已知A社区心理咨询满意率为0.85，B社区心理咨询满意率为0.95，C社区心理咨询满意率为0.9，“
，
，
”分别表示A，B，C社区的人们对心理咨询满意，“
，
，
”分别表示A，B，C社区的人们对心理咨询不满意，写出方差
，
，
的大小关系.（只需写出结论）
【题目】某市房管局为了了解该市市民2018年1月至2019年1月期间购买二手房情况，首先随机抽样其中200名购房者，并对其购房面积
（单位：万元/平方米，
进行了一次调查统计，制成了如图1所示的频率分布直方图，接着调查了该市2018年1月至2019年1月期间当月在售二手房均价
（单位：万元平方米），制成了如图2所示的散点图（图中月份代码1-13分别对应2018年1月至2019年1月）.
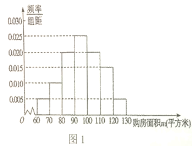
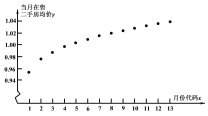
（1）试估计该市市民的平均购房面积
.
（2）现采用分层抽样的方法从购房面积位于
的40位市民中随机取4人，再从这4人中随机抽取2人，求这2人的购房面积恰好有一人在
的概率.
（3）根据散点图选
和
两个模型进行拟合，经过数据处理得到两个回归方程，分别为
和
，并得到一些统计量的值，如下表所示：
|
| |
| 0.000591 | 0.000164 |
| 0.00050 | |
请利用相关指数
判断哪个模型的拟合效果更好，并用拟合效果更好的模型预测2019年6月份的二手房购房均价（精确到0.001）./span>
参考数据：
，
，
，
，
，
，
，
，
参考公式：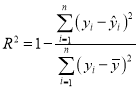
.
