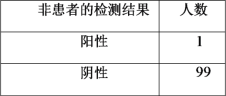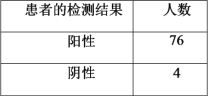题目内容
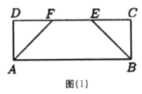
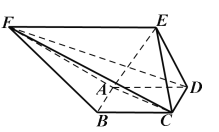
【题目】如图所示,边长为a的空间四边形ABCD中,∠BCD=90°,平面ABD⊥平面BCD,则异面直线AD与BC所成角的大小为( )
A. 30°B. 45°C. 60°D. 90°
【答案】C
【解析】
由题意得![]() ,
,![]() ,从而
,从而![]() ,
,![]() ,取
,取![]() 中点
中点![]() ,连结
,连结![]() ,
,![]() ,从而
,从而![]() 平面
平面![]() ,延长
,延长![]() 至点
至点![]() ,使
,使![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,则四边形
,则四边形![]() 为正方形,即有
为正方形,即有![]() ,从而
,从而![]() (或其补角)即为异面直线
(或其补角)即为异面直线![]() 与
与![]() 所成角,由此能求出异面直线
所成角,由此能求出异面直线![]() 与
与![]() 所成角的大小.
所成角的大小.
由题意得BC=CD=a,∠BCD=90°,
∴BD=![]() ,∴∠BAD=90°,
,∴∠BAD=90°,
取BD中点O,连结AO,CO,
∵AB=BC=CD=DA=a,
∴AO⊥BD,CO⊥BD,且AO=BO=OD=OC=![]() ,
,
又∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AO⊥BD,
∴AO⊥平面BCD,
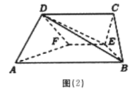
延长CO至点E,使CO=OE,连结ED,EA,EB,
则四边形BCDE为正方形,即有BC∥DE,
∴∠ADE(或其补角)即为异面直线AD与BC所成角,
由题意得AE=a,ED=a,
∴△AED为正三角形,∴∠ADE=60°,
∴异面直线AD与BC所成角的大小为60°.
故选:C.

【题目】某市房管局为了了解该市市民2018年1月至2019年1月期间购买二手房情况,首先随机抽样其中200名购房者,并对其购房面积![]() (单位:万元/平方米,
(单位:万元/平方米,![]() 进行了一次调查统计,制成了如图1所示的频率分布直方图,接着调查了该市2018年1月至2019年1月期间当月在售二手房均价
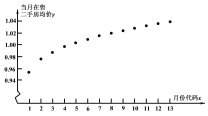
进行了一次调查统计,制成了如图1所示的频率分布直方图,接着调查了该市2018年1月至2019年1月期间当月在售二手房均价![]() (单位:万元平方米),制成了如图2所示的散点图(图中月份代码1-13分别对应2018年1月至2019年1月).
(单位:万元平方米),制成了如图2所示的散点图(图中月份代码1-13分别对应2018年1月至2019年1月).
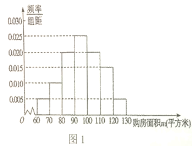
(1)试估计该市市民的平均购房面积![]() .
.
(2)现采用分层抽样的方法从购房面积位于![]() 的40位市民中随机取4人,再从这4人中随机抽取2人,求这2人的购房面积恰好有一人在
的40位市民中随机取4人,再从这4人中随机抽取2人,求这2人的购房面积恰好有一人在![]() 的概率.
的概率.
(3)根据散点图选![]() 和
和![]() 两个模型进行拟合,经过数据处理得到两个回归方程,分别为
两个模型进行拟合,经过数据处理得到两个回归方程,分别为![]() 和
和![]() ,并得到一些统计量的值,如下表所示:
,并得到一些统计量的值,如下表所示:
|
| |
| 0.000591 | 0.000164 |
| 0.00050 | |
请利用相关指数![]() 判断哪个模型的拟合效果更好,并用拟合效果更好的模型预测2019年6月份的二手房购房均价(精确到0.001)./span>
判断哪个模型的拟合效果更好,并用拟合效果更好的模型预测2019年6月份的二手房购房均价(精确到0.001)./span>
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
参考公式: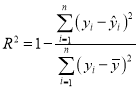 .
.
【题目】阿基米德是古希腊伟大的哲学家、数学家、物理学家,对几何学、力学等学科作出过卓越贡献.为调查中学生对这一伟大科学家的了解程度,某调查小组随机抽取了某市的100名高中生,请他们列举阿基米德的成就,把能列举阿基米德成就不少于3项的称为“比较了解”,少于三项的称为“不太了解”.他们的调查结果如下:
0项 | 1项 | 2项 | 3项 | 4项 | 5项 | 5项以上 | |
理科生(人) | 1 | 10 | 17 | 14 | 14 | 10 | 4 |
文科生(人) | 0 | 8 | 10 | 6 | 3 | 2 | 1 |
(1)完成如下![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为,了解阿基米德与选择文理科有关?
的把握认为,了解阿基米德与选择文理科有关?
比较了解 | 不太了解 | 合计 | |
理科生 | |||
文科生 | |||
合计 |
(2)在抽取的100名高中生中,按照文理科采用分层抽样的方法抽取10人的样本.
(i)求抽取的文科生和理科生的人数;
(ii)从10人的样本中随机抽取3人,用![]() 表示这3人中文科生的人数,求
表示这3人中文科生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() ,
,![]() .
.