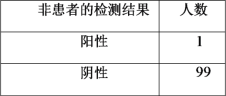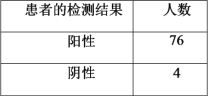题目内容
【题目】(1)已知f(x)=x3+3ax2+bx+a2在x=-1时有极值0,求常数a,b的值;
(2)设函数g(x)=x3-6x+5,x∈R. 若关于x的方程g(x)=m有三个不同的实根,求实数m的取值范围.
【答案】(1)a=2,b=9;(2)5-4![]() <a<5+4
<a<5+4![]() .
.
【解析】
(1)求出函数![]() 的导函数,由
的导函数,由![]() 在
在![]() 时有极值0,则
时有极值0,则![]() ,两式联立可求常数a,b的值;
,两式联立可求常数a,b的值;
(2)利用导数研究函数的单调性、极值,根据函数图象的大致形状可求出参数a的取值范围.
(1)由![]() 可得
可得![]() ,
,
因为![]() 在
在![]() 时有极值0,
时有极值0,
所以![]() ,
,
即![]() ,解得
,解得![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,
,
函数![]() 在R上单调递增,不满足在
在R上单调递增,不满足在![]() 时有极值,故舍去.
时有极值,故舍去.
所以常数a,b的值分别为![]() .
.
(2)![]() ,
,
令![]() ,解得
,解得![]() ,
,
![]() 当
当![]() 或
或![]() 时
时![]() ,当
,当![]() 时,
时,![]() ,
,
![]()
![]() 的递增区间是
的递增区间是![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() ,
,
当![]() 有极大值
有极大值![]() ,
,
当![]() 有极小值
有极小值![]() ,
,
由上分析可知y= f(x)图象的大致形状及走向,
![]() 当
当![]() 时,直线
时,直线![]() 与函数
与函数![]() 的图象有3个不同交点,
的图象有3个不同交点,
即方程g(x)=m有三个不同的实根

【题目】在抗击新冠肺炎疫情期间,很多人积极参与了疫情防控的志愿者活动.各社区志愿者服务类型有:现场值班值守,社区消毒,远程教育宣传,心理咨询(每个志愿者仅参与一类服务).参与A,B,C三个社区的志愿者服务情况如下表:
社区 | 社区服务总人数 | 服务类型 | |||
现场值班值守 | 社区消毒 | 远程教育宣传 | 心理咨询 | ||
A | 100 | 30 | 30 | 20 | 20 |
B | 120 | 40 | 35 | 20 | 25 |
C | 150 | 50 | 40 | 30 | 30 |
(1)从上表三个社区的志愿者中任取1人,求此人来自于A社区,并且参与社区消毒工作的概率;
(2)从上表三个社区的志愿者中各任取1人调查情况,以X表示负责现场值班值守的人数,求X的分布列;
(3)已知A社区心理咨询满意率为0.85,B社区心理咨询满意率为0.95,C社区心理咨询满意率为0.9,“![]() ,
,![]() ,
,![]() ”分别表示A,B,C社区的人们对心理咨询满意,“
”分别表示A,B,C社区的人们对心理咨询满意,“![]() ,
,![]() ,
,![]() ”分别表示A,B,C社区的人们对心理咨询不满意,写出方差
”分别表示A,B,C社区的人们对心理咨询不满意,写出方差![]() ,
,![]() ,
,![]() 的大小关系.(只需写出结论)
的大小关系.(只需写出结论)
【题目】2020年1月22日,国新办发布消息:新型冠状病毒来源于武汉一家海鲜市场非法销售的野生动.专家通过全基因组比对发现此病毒与2003年的非典冠状病毒以及此后的中东呼吸综合征冠状病毒,分别达到70%和40%的序列相似性.这种新型冠状病毒对人们的健康生命带来了严重威胁因此,某生物疫苗研究所加紧对新型冠状病毒疫苗进行实验,并将某一型号疫苗用在动物小白鼠身上进行科研和临床实验,得到统计数据如下:
未感染病毒 | 感染病毒 | 总计 | |
未注射疫苗 | 20 |
|
|
注射疫苗 | 30 |
|
|
总计 | 50 | 50 | 100 |
现从所有试验小白鼠中任取一只,取到“注射疫苗”小白鼠的概率为![]() .
.
(1)求![]() 列联表中的数据
列联表中的数据![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)能否有99.9%把握认为注射此种疫苗对预防新型冠状病毒有效?
附:![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |