题目内容
4．函数f（x）=$\frac{1}{{\sqrt{lg（3-x）}}}$的定义域是（-∞，2）．分析 由分母中根式内部的代数式大于0，然后求解对数不等式得答案．
解答 解：由lg（3-x）＞0，得3-x＞1，即x＜2．
∴函数f（x）=$\frac{1}{{\sqrt{lg（3-x）}}}$的定义域是（-∞，2）．
故答案为：（-∞，2）．
点评 本题考查函数的定义域及其求法，考查对数不等式的解法，是基础题．
练习册系列答案
相关题目
15．i是虚数单位，复数$\frac{i}{2+i}$=（ ）
| A． | $\frac{-1+2i}{3}$ | B． | $\frac{1+2i}{3}$ | C． | $\frac{1+2i}{5}$ | D． | $\frac{-1+2i}{5}$ |
12．对函数f（x）=$\sqrt{3}sinxcosx+{cos}^{2}x-\frac{1}{2}$的表述错误的是（ ）
| A． | 最小正周期为π | |
| B． | 函数y=sin2x向左平移$\frac{π}{12}$个单位可得到f（x） | |
| C． | f（x）在区间$（-\frac{π}{3}，\frac{π}{6}）$上递增 | |
| D． | 点$（\frac{π}{6}，0）$是f（x）的一个对称中心 |
如图所示，在正方体ABCD-A1B1C1D1中，E、G、H分别是BC、C1D1、AA1、的中点．
13．定义在R上的偶函数f（x）满足：对任意的x1，x2∈[0，+∞）（x1≠x2），有（x2-x1）[f（x2）-f（x1）]＜0．则（ ）
| A． | f（1）＜f（-2）＜f（3） | B． | f（3）＜f（1）＜f（-2） | C． | f（一2）＜f（1）＜f（3） | D． | f（3）＜f（-2）＜f（1） |
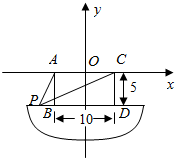船上两根高5m的桅杆相距10m，一条30m长的绳子两端系在桅杆的顶上，并按如图所示的方式绷紧，假设绳子位于两根桅杆所在的平面内，求绳子与甲板接触点P到桅杆AB的距离．