题目内容
(本小题满分14分)
已知数列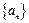 的前n项和为
的前n项和为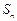 ,且
,且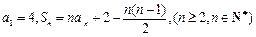
(1)求数列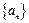 的通项公式;
的通项公式;
(2)设数列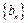 满足:
满足: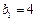 ,且
,且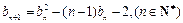 ,
,
求证: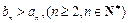 ;
;
(3)求证: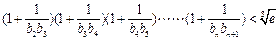 。
。
已知数列
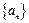 的前n项和为
的前n项和为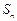 ,且
,且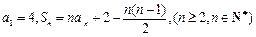
(1)求数列
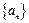 的通项公式;
的通项公式;(2)设数列
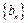 满足:
满足: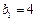 ,且
,且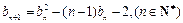 ,
,求证:
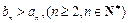 ;
;(3)求证:
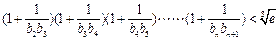 。
。(1)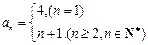
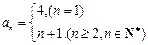
(1)当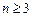 时,
时,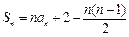 ,
,
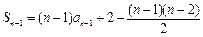 ,可得:
,可得: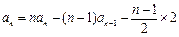
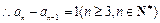 .
.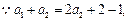
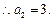
可得,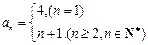
(2)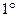 当
当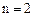 时,
时,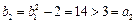 ,不等式成立.
,不等式成立.
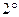 假设当
假设当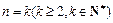 时,不等式成立,即
时,不等式成立,即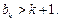 那么,当
那么,当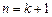 时,
时,
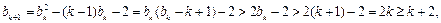
所以当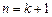 时,不等式也成立。
时,不等式也成立。
根据(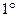 ),(
),(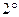 )可知,当
)可知,当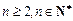 时,
时,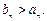
(3)设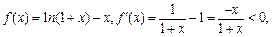
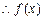 在
在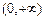 上单调递减,
上单调递减,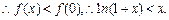
∵当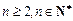 时,
时,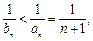
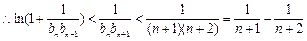 ,
,
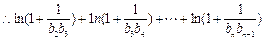
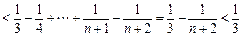
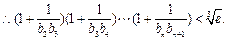
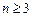 时,
时,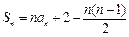 ,
,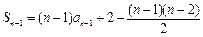 ,可得:
,可得: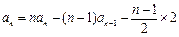
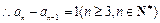 .
.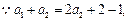
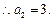
可得,
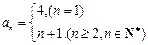
(2)
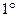 当
当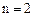 时,
时,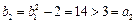 ,不等式成立.
,不等式成立. 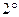 假设当
假设当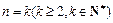 时,不等式成立,即
时,不等式成立,即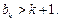 那么,当
那么,当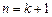 时,
时,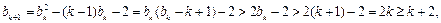
所以当
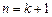 时,不等式也成立。
时,不等式也成立。根据(
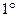 ),(
),(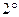 )可知,当
)可知,当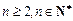 时,
时,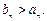
(3)设
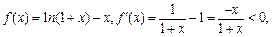
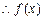 在
在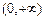 上单调递减,
上单调递减,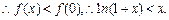
∵当
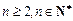 时,
时,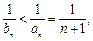
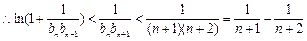 ,
,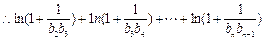
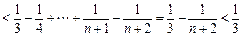
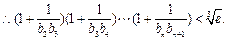

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
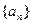 的首项为a1,公比q为正数(q≠1)的等比数列,其前n项和为Sn,且
的首项为a1,公比q为正数(q≠1)的等比数列,其前n项和为Sn,且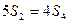 . (1)求q的值; (2)设
. (1)求q的值; (2)设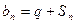 ,请判断数列
,请判断数列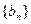 能否为等比数列,若能,请求出a1的值,否则请说明理由.
能否为等比数列,若能,请求出a1的值,否则请说明理由.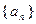 、
、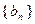 满足
满足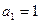 ,
,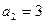 ,
,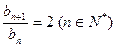 ,
,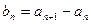 。
。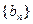 的通项公式;
的通项公式;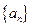 的通项公式;
的通项公式;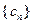 满足
满足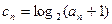
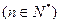 ,求
,求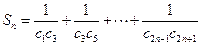 。
。 共有2m项,其中奇数项之和为90,偶数项之和为72,且
共有2m项,其中奇数项之和为90,偶数项之和为72,且 ,则该数列的公差为__________.
,则该数列的公差为__________.
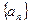 中,
中,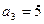 ,
,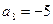 。
。
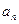 ;
;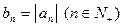 ,求数列
,求数列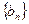 的前20项和
的前20项和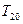 。
。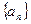 与等比数列
与等比数列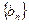 满足:
满足: ,
,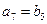 那么( )
那么( ) 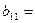
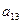
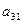
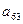
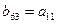
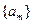 的前
的前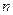 项和为
项和为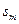 .若
.若 .
.