题目内容
1.已知函数f(x)=$\frac{1}{2}$x-sinx,x∈(0,π),则f(x)的最小值为$\frac{π}{6}$-$\frac{\sqrt{3}}{2}$.分析 先求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最小值.
解答 解:f′(x)=$\frac{1}{2}$-cosx,x∈(0,π),
令f′(x)<0,解得:0<x<$\frac{π}{3}$,令f′(x)>0,解得:$\frac{π}{3}$<x<π,
∴函数f(x)在(0,$\frac{π}{3}$)递减,在($\frac{π}{3}$,π)递增,
∴f(x)min=f($\frac{π}{3}$)=$\frac{π}{6}$-sin$\frac{π}{3}$=$\frac{π}{6}$-$\frac{\sqrt{3}}{2}$,
故答案为:$\frac{π}{6}$-$\frac{\sqrt{3}}{2}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道基础题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
12.命题“?x0∈∁RQ,x0∈Q”的否定是( )
| A. | ?x0∉∁RQ,x0∈Q | B. | ?x0∈∁RQ,x0∈Q | C. | ?x∉∁RQ,x∉Q | D. | ?x∈∁RQ,x∉Q |
9.函数y=$\frac{1}{2}$x+cosx在x∈[-$\frac{π}{2}$,$\frac{π}{2}$]上的最大值为$\frac{π}{12}$+$\frac{\sqrt{3}}{2}$.
16.某地四月份刮东风的概率是$\frac{8}{30}$,既刮东风又下雨的概率是$\frac{7}{30}$,则该地四月份刮东风的条件下,下雨的概率为( )
| A. | $\frac{8}{30}$ | B. | $\frac{7}{8}$ | C. | $\frac{1}{8}$ | D. | $\frac{7}{30}$ |
6.已知函数y=2cos(ωx+φ)(ω>0)在区间[0,2π]的图象如图,那么ω等于( )
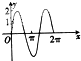

| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
13.集合A={(x,y)|y=lg(x+1)-1},B={(x,y)|x=m},若A∩B=∅,则实数m的取值范围是( )
| A. | (-∞,1) | B. | (-∞,1] | C. | (-∞,-1) | D. | (-∞,-1] |