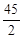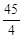题目内容
在直角坐标平面上有一点列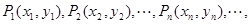 对一切正整数n,点
对一切正整数n,点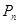 在函数
在函数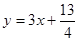 的图象上,且
的图象上,且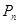 的横坐标构成以
的横坐标构成以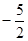 为首项,-1为公差的等差数列
为首项,-1为公差的等差数列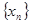 .
.
(Ⅰ)求点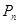 的坐标;
的坐标;
(Ⅱ)设抛物线列C1,C2,C3,…,Cn,…中的每一条的对称轴都垂直于x轴,抛物线Cn的顶点为Pn,且过点Dn(0,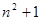 ).记与抛物线Cn相切于点Dn的直线的斜率为kn,求
).记与抛物线Cn相切于点Dn的直线的斜率为kn,求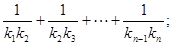
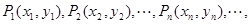 对一切正整数n,点
对一切正整数n,点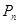 在函数
在函数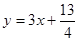 的图象上,且
的图象上,且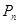 的横坐标构成以
的横坐标构成以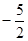 为首项,-1为公差的等差数列
为首项,-1为公差的等差数列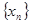 .
.(Ⅰ)求点
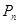 的坐标;
的坐标;(Ⅱ)设抛物线列C1,C2,C3,…,Cn,…中的每一条的对称轴都垂直于x轴,抛物线Cn的顶点为Pn,且过点Dn(0,
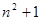 ).记与抛物线Cn相切于点Dn的直线的斜率为kn,求
).记与抛物线Cn相切于点Dn的直线的斜率为kn,求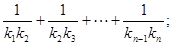
(Ⅰ)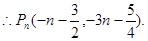 (Ⅱ)∴
(Ⅱ)∴ =
=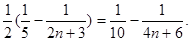
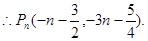 (Ⅱ)∴
(Ⅱ)∴ =
=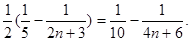
(I)由题意知 ,再根据点
,再根据点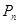 在函数
在函数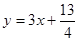 的图象上,可得点P的坐标.
的图象上,可得点P的坐标.
(2)解本小题的突破口是求出 的方程.因为
的方程.因为 的对称轴垂直于x轴,且顶点为Pn,
的对称轴垂直于x轴,且顶点为Pn,
设设 的方程为
的方程为 把点
把点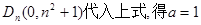 ,
,
∴ 的方程为
的方程为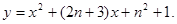
余下问题求导确定kn,进而可找到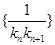 的通项公式确定出求和方法
的通项公式确定出求和方法
(Ⅰ) ,
,
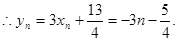
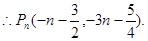 ………………4分
………………4分
(Ⅱ) 的对称轴垂直于x轴,且顶点为Pn,
的对称轴垂直于x轴,且顶点为Pn,
∴设 的方程为
的方程为
把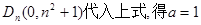 ,………………7分
,………………7分
∴ 的方程为
的方程为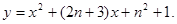 ………………8分
………………8分
∵
∴ …………10分
…………10分
∴
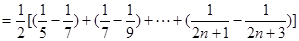
=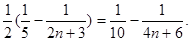
 ,再根据点
,再根据点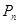 在函数
在函数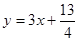 的图象上,可得点P的坐标.
的图象上,可得点P的坐标.(2)解本小题的突破口是求出
 的方程.因为
的方程.因为 的对称轴垂直于x轴,且顶点为Pn,
的对称轴垂直于x轴,且顶点为Pn,设设
 的方程为
的方程为 把点
把点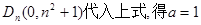 ,
,∴
 的方程为
的方程为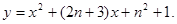
余下问题求导确定kn,进而可找到
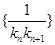 的通项公式确定出求和方法
的通项公式确定出求和方法(Ⅰ)
 ,
,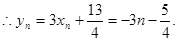
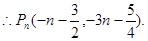 ………………4分
………………4分(Ⅱ)
 的对称轴垂直于x轴,且顶点为Pn,
的对称轴垂直于x轴,且顶点为Pn,∴设
 的方程为
的方程为
把
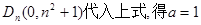 ,………………7分
,………………7分∴
 的方程为
的方程为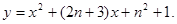 ………………8分
………………8分∵

∴
 …………10分
…………10分∴

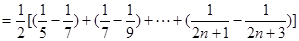
=
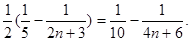

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
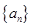 的前
的前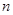 项和为
项和为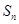 ,且满足
,且满足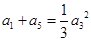 ,
,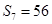 .
.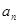 ;
;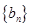 满足
满足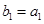 且
且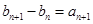 ,求数列
,求数列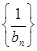 的前
的前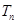 .
.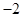 的等差数列
的等差数列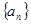 的前
的前 项和为
项和为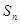 ,且
,且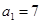 ,则使
,则使 成立的最小的自然数
成立的最小的自然数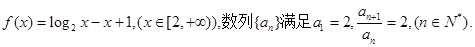
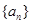 的通项公式
的通项公式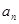 ;
;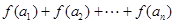 ;
;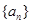 为等差数列,
为等差数列,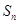 为其前n项和,若
为其前n项和,若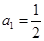 ,
,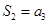 ,则
,则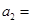 ,
,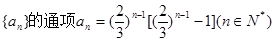 ,则下列表述正确的是
,则下列表述正确的是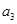
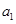 ,最小项不存在
,最小项不存在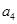
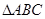 的三内角
的三内角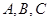 成等差数列,且
成等差数列,且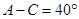 ,则
,则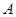 = .
= .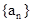 中,已知前15项的和
中,已知前15项的和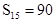 ,则
,则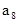 等于( ).
等于( ).