题目内容
如图所示,多面体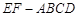 中,
中, 是梯形,
是梯形,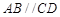 ,
, 是矩形,平面
是矩形,平面 平面
平面 ,
, ,
,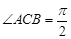 .
.

(1)求证: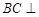 平面
平面 ;
;
(2)若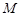 是棱
是棱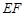 上一点,
上一点,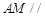 平面
平面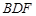 ,求
,求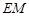 ;
;
(3)求二面角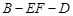 的平面角的余弦值.
的平面角的余弦值.
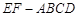 中,
中, 是梯形,
是梯形,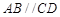 ,
, 是矩形,平面
是矩形,平面 平面
平面 ,
, ,
,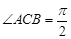 .
.
(1)求证:
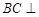 平面
平面 ;
;(2)若
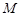 是棱
是棱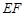 上一点,
上一点,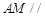 平面
平面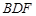 ,求
,求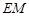 ;
;(3)求二面角
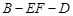 的平面角的余弦值.
的平面角的余弦值.(1)见解析 (2) . (3)
. (3) .
.
 . (3)
. (3) .
.(1)易证: ,再根据平面ACFE
,再根据平面ACFE 平面ABCD,利用面面垂直的性质定理转化为
平面ABCD,利用面面垂直的性质定理转化为 .
.
(2)连接BD,交AC于O点,若 则
则 .从而再根据O的位置确定M的位置求出EM的长度.
.从而再根据O的位置确定M的位置求出EM的长度.
(3)以C为原点,CA、CB、CF分别为x轴,y轴,z轴建立空间直角坐标系C-xyz,然后分别求出平面BEF和平面EFD的法向量,利用向量法求二面角B-EF-D的平面角的余弦值
(1)平面 ,
,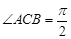 ,从而
,从而 .又因为
.又因为 面
面 ,平面
,平面 平面
平面 ,所以
,所以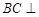 平面
平面 .
.
(2)连接 ,记
,记 ,在梯形
,在梯形 中,因为
中,因为 ,
,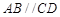 ,所以
,所以 ,
, ,
, ,从而
,从而 .又因为
.又因为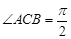 ,
, ,所以
,所以 .连接
.连接 ,由
,由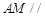 平面
平面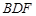 得
得 ,因为
,因为 是矩形,所以
是矩形,所以 .
.
(3)以 为原点,
为原点, 、
、 、
、 分别为
分别为 轴、
轴、 轴、
轴、 轴建立空间直角坐标系
轴建立空间直角坐标系 ,则
,则 ,
, ,
, ,
, ,
, ,
, ,设平面
,设平面 的一个法向量为
的一个法向量为 ,则有
,则有 ,即
,即 ,解得
,解得 .
.
同理可得平面 的一个法向量为
的一个法向量为 ,观察知二面角
,观察知二面角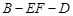 的平面角为锐角,所以其余弦值为
的平面角为锐角,所以其余弦值为 .
.
 ,再根据平面ACFE
,再根据平面ACFE 平面ABCD,利用面面垂直的性质定理转化为
平面ABCD,利用面面垂直的性质定理转化为 .
.(2)连接BD,交AC于O点,若
 则
则 .从而再根据O的位置确定M的位置求出EM的长度.
.从而再根据O的位置确定M的位置求出EM的长度.(3)以C为原点,CA、CB、CF分别为x轴,y轴,z轴建立空间直角坐标系C-xyz,然后分别求出平面BEF和平面EFD的法向量,利用向量法求二面角B-EF-D的平面角的余弦值
(1)平面
 ,
,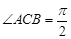 ,从而
,从而 .又因为
.又因为 面
面 ,平面
,平面 平面
平面 ,所以
,所以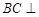 平面
平面 .
.(2)连接
 ,记
,记 ,在梯形
,在梯形 中,因为
中,因为 ,
,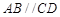 ,所以
,所以 ,
, ,
, ,从而
,从而 .又因为
.又因为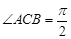 ,
, ,所以
,所以 .连接
.连接 ,由
,由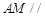 平面
平面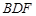 得
得 ,因为
,因为 是矩形,所以
是矩形,所以 .
.(3)以
 为原点,
为原点, 、
、 、
、 分别为
分别为 轴、
轴、 轴、
轴、 轴建立空间直角坐标系
轴建立空间直角坐标系 ,则
,则 ,
, ,
, ,
, ,
, ,
, ,设平面
,设平面 的一个法向量为
的一个法向量为 ,则有
,则有 ,即
,即 ,解得
,解得 .
.同理可得平面
 的一个法向量为
的一个法向量为 ,观察知二面角
,观察知二面角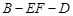 的平面角为锐角,所以其余弦值为
的平面角为锐角,所以其余弦值为 .
.
练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
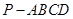 中,
中,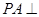 平面
平面 四边形
四边形 为正方形,
为正方形,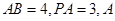 点在
点在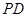 上的射影为
上的射影为 点.
点.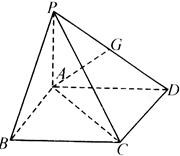
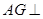 平面
平面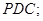
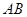 上是否存在一点
上是否存在一点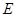 ,使得
,使得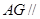 平面
平面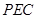 .若存在,求出
.若存在,求出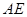 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
 BC,AC=BC=4,四边形ABDE是直角梯形,BD
BC,AC=BC=4,四边形ABDE是直角梯形,BD AE,BD
AE,BD
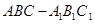 中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则
中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则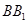 与平面
与平面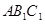 所成的角的大小为
所成的角的大小为 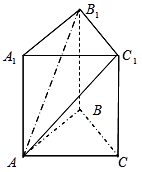
 表示平面,则以下命题正确的有( )
表示平面,则以下命题正确的有( ) ; ②
; ② ; ③
; ③ ; ④
; ④ .
. 为不重合的平面,
为不重合的平面, 为不重合的直线,则下列命题正确的是( )
为不重合的直线,则下列命题正确的是( ) ,
, ,
, ,则
,则
 ,
, ,
, ,则
,则
 ,
, ,
, ,
, ,
, ,则
,则 ,则这个长方体的对角线长为__________
,则这个长方体的对角线长为__________