题目内容
(本题满分14分)如图, 在直三棱柱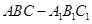 中,
中,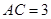 ,
,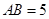 ,
,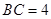
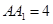 ,点
,点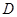 是
是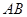 的中点.
的中点.
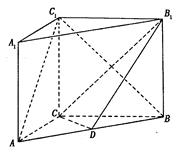
⑴求证: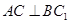 ;
;
⑵求证: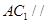 平面
平面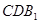 ;
;
⑶求二面角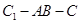 的正切值.
的正切值.
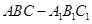 中,
中,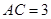 ,
,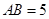 ,
,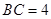
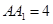 ,点
,点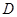 是
是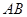 的中点.
的中点.
⑴求证:
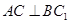 ;
;⑵求证:
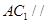 平面
平面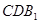 ;
;⑶求二面角
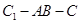 的正切值.
的正切值.⑴见解析;⑵见解析;⑶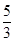
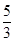
本试题主要考查了立体几何中的线线垂直的证明,以及线面平行的判定和二面角的平面角的求解的综合运用。
(1)由于已知中三棱柱的性质和三角形可知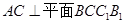 ,得到结论。
,得到结论。
(2)利用线线平行来判定得到线面平行的证明。
(3)由于二面角的平面角可以建立空间直角坐标系,求解平面的法向量来表示夹角得到二面角 平面角的求解。
证明:⑴、在直三棱柱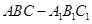 ,
,
∵底面三边长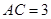 ,
,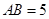 ,
,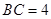 ,∴
,∴ 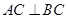 ,………1分
,………1分
又直三棱柱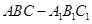 中,
中,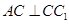 ,且
,且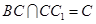 ,
,
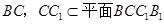 ,∴
,∴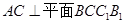 .……………3分
.……………3分
而 ,∴
,∴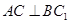 ;…………………………4分
;…………………………4分
⑵、设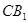 与
与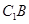 的交点为
的交点为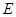 ,连结
,连结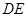 ,…5分
,…5分
∵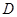 是
是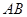 的中点,
的中点,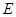 是
是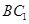 的中点,∴
的中点,∴ 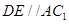 ,………7分
,………7分
∵ ,
,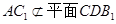 ,∴
,∴ .…8分
.…8分
⑶、过点C作CF⊥AB于F,连接C1F.…………9分
由已知C1C垂直平面ABC,
则∠C1FC为二面角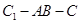 的平面角。………11分
的平面角。………11分
在Rt△ABC中,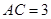 ,
,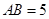 ,
,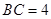 ,则
,则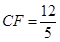 …………12分
…………12分
又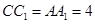 ,∴
,∴ 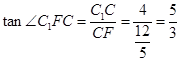 ,……………13分
,……………13分
∴二面角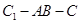 的正切值为
的正切值为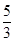 .…………………………14分
.…………………………14分
(另:可以建立空间直角坐标系用向量方法完成,酌情给分,过程略)
(1)由于已知中三棱柱的性质和三角形可知
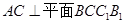 ,得到结论。
,得到结论。(2)利用线线平行来判定得到线面平行的证明。
(3)由于二面角的平面角可以建立空间直角坐标系,求解平面的法向量来表示夹角得到二面角 平面角的求解。
证明:⑴、在直三棱柱
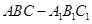 ,
,∵底面三边长
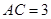 ,
,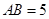 ,
,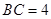 ,∴
,∴ 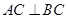 ,………1分
,………1分又直三棱柱
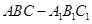 中,
中,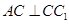 ,且
,且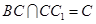 ,
,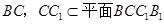 ,∴
,∴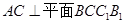 .……………3分
.……………3分而
 ,∴
,∴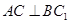 ;…………………………4分
;…………………………4分⑵、设
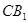 与
与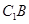 的交点为
的交点为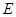 ,连结
,连结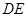 ,…5分
,…5分∵
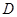 是
是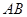 的中点,
的中点,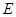 是
是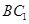 的中点,∴
的中点,∴ 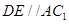 ,………7分
,………7分∵
 ,
,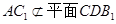 ,∴
,∴ .…8分
.…8分⑶、过点C作CF⊥AB于F,连接C1F.…………9分
由已知C1C垂直平面ABC,
则∠C1FC为二面角
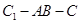 的平面角。………11分
的平面角。………11分在Rt△ABC中,
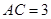 ,
,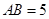 ,
,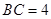 ,则
,则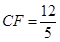 …………12分
…………12分又
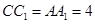 ,∴
,∴ 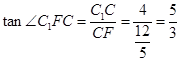 ,……………13分
,……………13分∴二面角
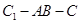 的正切值为
的正切值为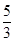 .…………………………14分
.…………………………14分(另:可以建立空间直角坐标系用向量方法完成,酌情给分,过程略)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
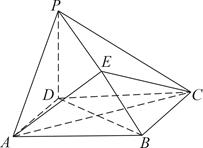
 AB且E为PB的中点时,求AE与平面PDB所成角的大小。
AB且E为PB的中点时,求AE与平面PDB所成角的大小。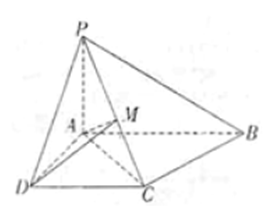
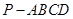 中,
中,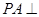 平面
平面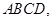 四边形
四边形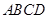 为正方形,
为正方形,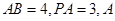 点在
点在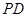 上的射影为
上的射影为 点.
点.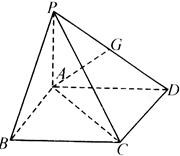
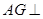 平面
平面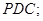
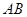 上是否存在一点
上是否存在一点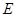 ,使得
,使得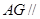 平面
平面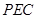 .若存在,求出
.若存在,求出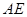 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.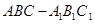 中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则
中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则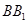 与平面
与平面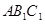 所成的角的大小为
所成的角的大小为 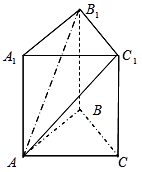
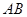 是圆
是圆 的直径,
的直径,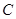 是异于
是异于 ,
, 两点的圆周上的任意一点,
两点的圆周上的任意一点, 垂直于圆
垂直于圆 ,
,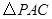 ,
,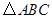 ,
,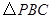 中,直角三角形的个数是( )
中,直角三角形的个数是( )
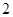
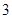
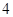

 、
、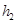 、
、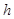 ,则
,则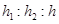 等于( )
等于( )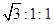

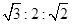

 表示平面,则以下命题正确的有( )
表示平面,则以下命题正确的有( ) ; ②
; ② ; ③
; ③ ; ④
; ④ .
.