题目内容
17.已知数列{an}的前n项和为Sn,满足2Sn=n(an+4)(n∈N*)(I)设a2=5,求a4;
(Ⅱ)设a2=t,若当且仅当n=5时Sn取得最大值,求实数t的取值范围.
分析 (I)通过对2Sn=n(an+4)(n∈N*)中令n=1,3,4,结合a2=5计算即得结论;
(Ⅱ)通过2Sn=n(an+4)(n∈N*)可得当n≥2时,有2Sn-1=(n-1)(an-1+4)(n∈N*),两者相减可得(n-2)an=(n-1)an-1-4,进而有(n-1)an+1=nan-4,两者相减可得数列{an}为等差数列,计算即得结论.
解答 解:(I)∵2Sn=n(an+4)(n∈N*),a2=5,
∴当n=1时,可得a1=4;
当n=3时,2(a1+a2+a3)=2(4+5+a3)=3(a3+4),即a3=6;
当n=4时,可得2(a1+a2+a3+a4)=2(4+5+6+a4)=3(4+a4),即a4=7;
(Ⅱ)∵2Sn=n(an+4)(n∈N*),
∴当n≥2时,有2Sn-1=(n-1)(an-1+4)(n∈N*),
两式相减可得:2an=nan-(n-1)an-1+4,
即(n-2)an=(n-1)an-1-4,
又∵(n-1)an+1=nan-4,
两式相减可得:(n-1)an+1+(n-1)an-1=(2n-2)an(n≥2),
∴an+1+an-1=2an(n≥2),
即an+1-an=an-an-1(n≥2),即数列{an}为等差数列,
在2Sn=n(an+4)中令n=1可得a1=4,
又a2=t,∴数列{an}的公差为t-4,
∴an=(t-4)n+8-t,
当且仅当n=5时,Sn取得最大值,等价于a5>0且a6<0,
即t>3,且t<$\frac{16}{5}$,故t∈(3,$\frac{16}{5}$).
点评 本题考查是一道关于数列的综合题,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
7.设集合M={x∈R|x2=1},N={x∈R|x2-2x-3=0},则M∪N=( )
| A. | {-1} | B. | {-1,1,3} | C. | {1,3} | D. | {-1,3} |
8.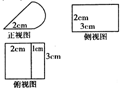 某几何体的三视图如图所示,其正视图中的曲线部分为半圆,则该几何体的表面积为( )
某几何体的三视图如图所示,其正视图中的曲线部分为半圆,则该几何体的表面积为( )
 某几何体的三视图如图所示,其正视图中的曲线部分为半圆,则该几何体的表面积为( )
某几何体的三视图如图所示,其正视图中的曲线部分为半圆,则该几何体的表面积为( )| A. | 10+6$\sqrt{2}$+4π(cm2) | B. | 16+6$\sqrt{2}$+4π(cm2) | C. | 12+4π(cm2) | D. | 22+4π(cm2) |
5.已知平面α∥β,且α与β的距离为d(d>0). m?α.则在β内与直线m的距离为2d的直线共有( )
| A. | 0条 | B. | 1条 | C. | 2条 | D. | 无数条 |
12.已知a=sin2,b=log${\;}_{\frac{1}{3}}$2,c=log${\;}_{\frac{1}{2}}$$\frac{1}{3}$,则( )
| A. | a>b>c | B. | c>a>b | C. | a>c>b | D. | c>b>a |
2.某高中有高一新生500名,分成水平相同的A,B两类进行教学实验.为对比教学效果,现用分层抽样的方法从A、B两类学生中分别抽取了40人、60人进行测试.
(Ⅰ)求该学校高一新生A、B两类学生各多少人?
(Ⅱ)经过测试,得到以下三个数据图表:
图一:75分以上A、B两类参加测试学生成绩的茎叶图(茎、叶分别是十位和个位上的数字)(如图1)
图二:100名测试学生成绩的频率分布直方图2;

表一:100名测试学生成绩频率分布表;
①先填写频率分布表(表一)中的六个空格,然后将频率分布直方图(图二)补充完整;
②该学校拟定从参加考试的79分以上(含79分)的B类学生中随机抽取2人代表学校参加市比赛,求抽到的2人分数都在80分以上的概率.
(Ⅰ)求该学校高一新生A、B两类学生各多少人?
(Ⅱ)经过测试,得到以下三个数据图表:
图一:75分以上A、B两类参加测试学生成绩的茎叶图(茎、叶分别是十位和个位上的数字)(如图1)
图二:100名测试学生成绩的频率分布直方图2;

表一:100名测试学生成绩频率分布表;
| 组号 | 分组 | 频数 | 频率 |
| 1 | [55,60) | 5 | 0.05 |
| 2 | [60,65) | 20 | 0.20 |
| 3 | [65,70) | ||
| 4 | [70,75) | 35 | 0.35 |
| 5 | [75,80) | ||
| 6 | [80,85) | ||
| 合计 | 100 | 1.00 | |
②该学校拟定从参加考试的79分以上(含79分)的B类学生中随机抽取2人代表学校参加市比赛,求抽到的2人分数都在80分以上的概率.
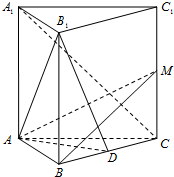 在正三棱柱ABC-A1B1C1中,点D是BC的中点.
在正三棱柱ABC-A1B1C1中,点D是BC的中点.