Question

【题目】设实数x，y满足条件 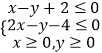，若目标函数z=ax+by（a＞0，b＞0）的最大值为12，则 的最小值为 ．

Answer 1

【答案】
【解析】解：由z=ax+by（a＞0，b＞0）得y= ，
作出可行域如图：
∵a＞0，b＞0，
∴直线y= 的斜率为负，且截距最大时，z也最大．
平移直线y= ，由图象可知当y= 经过点A时，
直线的截距最大，此时z也最大．
由 ，解得 ，即A（6，8）．
此时z=6a+8b=12，
即 + =1，
则 =（ ）（ + ）
= + + + ≥ +2 = +4= ，
当且仅当 = 时取=号，
故答案为：

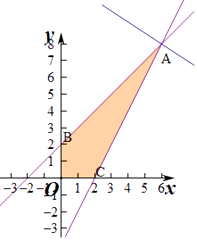
作出不等式对应的平面区域，利用线性规划的知识先求出a，b的关系，然后利用基本不等式求 的最小值．