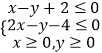题目内容
【题目】已知函数 ![]() ,其中a为常数,
,其中a为常数,
(1)若函数f(x)为奇函数,求a的值;
(2)若函数f(x)在(2,5)上有意义,求实数a的取值范围.
【答案】
(1)解:因为f(x)为奇函数,所以f(﹣x)+f(x)=0对定义域内的任意x恒成立,
即 ![]() 对定义域内的任意x恒成立,
对定义域内的任意x恒成立,
故 ![]() ,即(a2﹣1)x2=0对定义域内的任意x恒成立,
,即(a2﹣1)x2=0对定义域内的任意x恒成立,
故a2﹣1=0,即a=±1…(3分)
当a=1时, ![]() 为奇函数,满足条件;
为奇函数,满足条件;
当a=﹣1时, ![]() 无意义,故不成立.
无意义,故不成立.
综上,a=1
(2)解:若f(x)在(2,5)内恒有意义,则当x∈(2,5)时,有 ![]() 恒成立,
恒成立,
因为x>2,所以x+3>0,从而ax﹣3>0在x∈(2,5)上恒成立,
令g(x)=ax﹣3,则
当a=0时,不合题意
当a≠0时, ![]() ,解得
,解得 ![]() ,
,
所以,实数a的取值范围是 ![]()
【解析】(1)由奇函数的定义可求出a的值,经讨论舍去a=﹣1。(2)根据题意可得到ax﹣3>0在x∈(2,5)上恒成立,构造函数利用其x∈(2,5)上恒成立,得到不等式组解得a的取值范围。
【考点精析】解答此题的关键在于理解函数的奇偶性的相关知识,掌握偶函数的图象关于y轴对称;奇函数的图象关于原点对称.

练习册系列答案
相关题目