题目内容
(本题满分12分)已知函数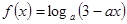
(1)当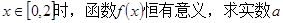 的取值范围;
的取值范围;
(2)是否存在这样的实数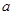 ,使得函数
,使得函数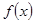 在区间
在区间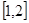 上为减函数,且最大值为1,若存在,求出
上为减函数,且最大值为1,若存在,求出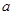 值;若不存在,说明理由。
值;若不存在,说明理由。
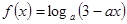
(1)当
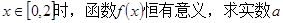 的取值范围;
的取值范围;(2)是否存在这样的实数
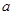 ,使得函数
,使得函数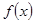 在区间
在区间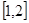 上为减函数,且最大值为1,若存在,求出
上为减函数,且最大值为1,若存在,求出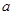 值;若不存在,说明理由。
值;若不存在,说明理由。(1)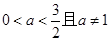 ;(2)这样的
;(2)这样的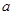 不存在。
不存在。
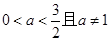 ;(2)这样的
;(2)这样的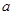 不存在。
不存在。试题分析:(1)根据对数函数有意义可知,真数部分
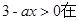
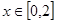 上恒成立,即
上恒成立,即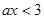 ,得到a的范围。
,得到a的范围。(2)假设存在这样的
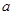
设
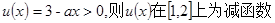 ,且有
,且有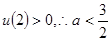 ,可知外层为增函数,得到a的范围,进而求解最值。
,可知外层为增函数,得到a的范围,进而求解最值。解:(1)
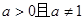 ,
, 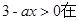
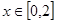 上恒成立,即
上恒成立,即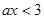
当

当
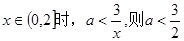
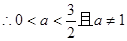 …………..4分
…………..4分(2)假设存在这样的
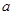
设
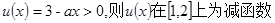 ,且有
,且有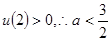 ………..6分
………..6分则
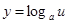 在区间内为增函数,
在区间内为增函数,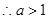 即
即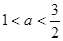 ………………8分
………………8分而
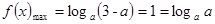
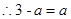
 …………..10分
…………..10分 内,所以这样的
内,所以这样的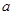 不存在……………12分
不存在……………12分点评:解决该试题的关键是根据已知中恒有意义说明了最小值处 函数值大于零,同时根据存在a使得函数递减,则利用同增异减的思想得到a的取值情况。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
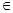 (0,π)恒成立?若存在,请求出a的范围;若不存在,请说明理由.
(0,π)恒成立?若存在,请求出a的范围;若不存在,请说明理由. 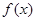 =
=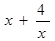
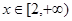 上是增函数;(2)求
上是增函数;(2)求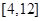 上的值域。
上的值域。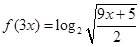 ,那么
,那么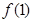 =_____________。
=_____________。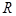 上的奇函数
上的奇函数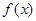 对任意
对任意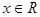 都有
都有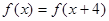 ,当
,当 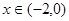 时,
时,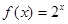 ,则
,则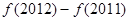 的值为( )
的值为( )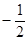
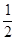
 2
2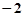
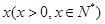 户农民从事蔬菜加工,则剩下的继续从事蔬菜种植的农民平均每户的年收入有望提高
户农民从事蔬菜加工,则剩下的继续从事蔬菜种植的农民平均每户的年收入有望提高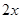 %,而从事蔬菜加工的农民平均每户的年收入将为
%,而从事蔬菜加工的农民平均每户的年收入将为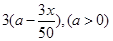 万元.
万元.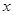 户农民从事蔬菜加工后,要使从事蔬菜种植的农民的总年收入不低于动员前从事蔬菜种植的农民的总年收入,求
户农民从事蔬菜加工后,要使从事蔬菜种植的农民的总年收入不低于动员前从事蔬菜种植的农民的总年收入,求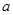 的最大值.
的最大值.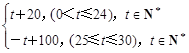 ;该商品的日销售量Q(件)与时间(天)的函数关系式为:
;该商品的日销售量Q(件)与时间(天)的函数关系式为: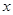 万美元,可获得加工费近似为
万美元,可获得加工费近似为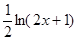 万美元,受美联储货币政策的影响,美元贬值,由于生产加工签约和成品交付要经历一段时间,收益将因美元贬值而损失
万美元,受美联储货币政策的影响,美元贬值,由于生产加工签约和成品交付要经历一段时间,收益将因美元贬值而损失 万美元,其中
万美元,其中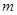 为该时段美元的贬值指数,
为该时段美元的贬值指数,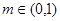 ,从而实际所得的加工费为
,从而实际所得的加工费为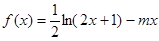 (万美元).
(万美元).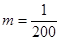 ,为确保企业实际所得加工费随
,为确保企业实际所得加工费随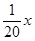 万美元,已知该企业加工生产能力为
万美元,已知该企业加工生产能力为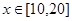 (其中
(其中