题目内容
某企业为打入国际市场,决定从A、B两种产品中只选择一种进行投资生产.已
知投资生产这两种产品的有关数据如下表:(单位:万美元)
其中年固定成本与年生产的件数无关,m为待定常数,其值由生产A产品的原材料价格决定,预计m∈[3,4].另外,年销售x件B产品时需上交0.05x2万美元的特别关税.假设生产出来的产品都能在当年销售出去.
(1)写出该厂分别投资生产A、B两种产品的年利润y1,y2与生产相应产品的件数x之间的函数关系并指明其定义域;
(2)如何投资才可获得最大年利润?请你做出规划.
知投资生产这两种产品的有关数据如下表:(单位:万美元)
| 项目类别 | 年固定成本 | 每件产品成本 | 每件产品销售价 | 每年最多可生产的件数 |
| A产品 | 10 | m | 5 | 100 |
| B产品 | 20 | 4 | 9 | 60 |
(1)写出该厂分别投资生产A、B两种产品的年利润y1,y2与生产相应产品的件数x之间的函数关系并指明其定义域;
(2)如何投资才可获得最大年利润?请你做出规划.
(1)y1=(5-m)x-10,0<x≤100,且x∈N,y2=-0.05x2+5x-20,0<x≤60且x∈N;
(2)当3≤m<3.85投资A产品200件可获得最大利润;当3.85<m≤4投资B产品100件可获得最大利润;m=3.85生产A产品与B产品均可获得最大年利润。
(2)当3≤m<3.85投资A产品200件可获得最大利润;当3.85<m≤4投资B产品100件可获得最大利润;m=3.85生产A产品与B产品均可获得最大年利润。
试题分析:(1)y1=5x-(10+mx)=(5-m)x-10,0<x≤100,且x∈N
y2=9x-(4x+20)-0.05x2=-0.05x2+5x-20,0<x≤60且x∈N
(2)∵3≤m≤4∴5-m>0∴y1=(5-m)x-10为增函数
又0≤x≤100,x∈N∴x=100时,生产A产品有最大利润(5-m)×100-10=490-100m(万美元)
y2=-0.05x2+5x-20=-0.05(x-50)2+105,0≤x≤60,x∈N
∴x=50时,生产B产品有最大利润105(万美元)(y1)max-(y2)max="490-100m" -105=385-100 m
当3≤m<3.85时,(y1)max-(y2)max>0
当m=3.85时,(y1)max-(y2)max=0
当3.85<m≤4时,(y1)max-(y2)max<0
∴当3≤m<3.85投资A产品200件可获得最大利润
当3.85<m≤4投资B产品100件可获得最大利润
m=3.85生产A产品与B产品均可获得最大年利润
点评:考查把实际问题转化为抽象函数模型的能力,并能根据模型的解决,指导实际生活中的决策问题,属中档题.

练习册系列答案
相关题目
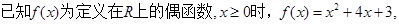
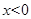 时函数的解析式
时函数的解析式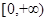 上是单调递增
上是单调递增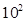 kg)与上市时间t(单位:天)的数据如下表:
kg)与上市时间t(单位:天)的数据如下表: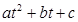 , Q= a
, Q= a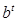 , Q=a
, Q=a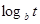 .
.
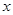 ,符号
,符号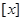 表示不超过
表示不超过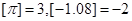 ,定义函数
,定义函数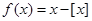 ,则下列命题中正确的是( )
,则下列命题中正确的是( )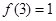
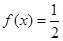 有且仅有一个解
有且仅有一个解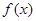 是周期函数
是周期函数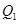 和日产量
和日产量 均为价格
均为价格 的函数,且
的函数,且
 ,日成本C关于日产量
,日成本C关于日产量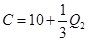
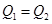 时的价格为均衡价格,求均衡价格
时的价格为均衡价格,求均衡价格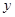 最大,求
最大,求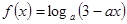
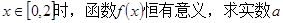 的取值范围;
的取值范围;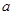 ,使得函数
,使得函数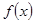 在区间
在区间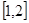 上为减函数,且最大值为1,若存在,求出
上为减函数,且最大值为1,若存在,求出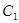 的方程是
的方程是
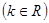 ,曲线
,曲线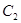 的方程是
的方程是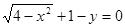 ,给出下列结论:
,给出下列结论: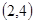 ;
;  ②曲线
②曲线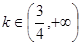 时,
时,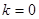 时,则
时,则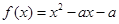 ,
,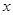 ,使得
,使得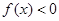 ,求实数
,求实数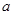 的取值范围;
的取值范围;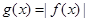 ,且
,且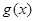 在区间
在区间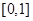 上单调递增,求实数
上单调递增,求实数