题目内容
【题目】已知函数 ![]() .
.
(1)求证:f(x)在(0,+∞)上是单调递增函数;
(2)若f(x)在 ![]() 上的值域是
上的值域是 ![]() ,求a的值.
,求a的值.
【答案】
(1)证明:证明:设x2>x1>0,则x2﹣x1>0,x1x2>0,
∵ 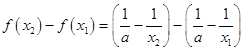 =
= ![]() ,
,
∴f(x2)>f(x1),
∴f(x)在(0,+∞)上是单调递增的
(2)证明:∵f(x)在(0,+∞)上是单调递增的,
∴f(x)在 ![]() 上单调递增,
上单调递增,
∴ ![]() ,
,
∴ ![]()
【解析】(1)利用函数单调性的定义,设x2>x1>0,再将f(x1)﹣f(x2)作差后化积,证明即可;(2)由(1)知f(x)在(0,+∞)上是单调递增的,从而在[ ![]() ,2]上单调递增,由f(2)=2可求得a的值.
,2]上单调递增,由f(2)=2可求得a的值.
【考点精析】掌握函数单调性的判断方法和函数单调性的性质是解答本题的根本,需要知道单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集.

 名校课堂系列答案
名校课堂系列答案【题目】某校计划面向高一年级![]() 名学生开设校本选修课程,为确保工作的顺利实施,先按性别进行分层抽样,抽取了
名学生开设校本选修课程,为确保工作的顺利实施,先按性别进行分层抽样,抽取了![]() 名学生对社会科学类,自然科学类这两大类校本选修课程进行选课意向调查,其中男生有
名学生对社会科学类,自然科学类这两大类校本选修课程进行选课意向调查,其中男生有![]() 人.在这
人.在这![]() 名学生中选择社会科学类的男生、女生均为
名学生中选择社会科学类的男生、女生均为![]() 人.
人.
(Ⅰ)分别计算抽取的样本中男生及女生选择社会科学类的频率,并以统计的频率作为概率,估计实际选课中选择社会科学类学生数;
(Ⅱ)根据抽取的![]() 名学生的调查结果,完成下列列联表.并判断能否在犯错误的概率不超过
名学生的调查结果,完成下列列联表.并判断能否在犯错误的概率不超过![]() 的前提下认为科类的选择与性别有关?
的前提下认为科类的选择与性别有关?
选择自然科学类 | 选择社会科学类 | 合计 | |
男生 | |||
女生 | |||
合计 |
附: 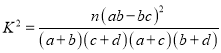 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
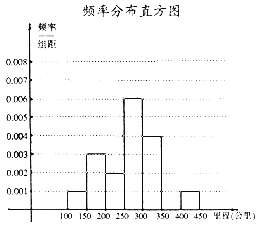
【题目】面对全球范围内日益严峻的能源形势与环保压力,环保与低碳成为今后汽车发展的一大趋势,越来越多的消费者对新能源汽车表示出更多的关注,某研究机构从汽车市场上随机抽取N辆纯电动汽车调查其续航里程(单次充电后能行驶的最大里程),被调查汽车的续航里程全部介于100公里和450公里之间,根据调查数据形成了如图所示频率分布表及频率分布直方图.
频率分布表
分组 | 频数 | 频率 |
[100,150) | 1 | 0.05 |
[150,200) | 3 | 0.15 |
[200,250) | x | 0.1 |
[250,300) | 6 | 0.3 |
[300,350) | 4 | 0.2 |
[350,400) | 3 | y |
[400,450] | 1 | 0.05 |
合计 | N | 1 |
(1)试确定频率分布表中x,y,N的值,并补全频率分布直方图;
(2)若从续航里程在[200,250)及[350,400)的车辆中随机抽取2辆车,求两辆车续航里程都在[350,400)的概率.