题目内容
在等差数列{an}中，a3＋a4＋a5＝84，a9＝73.
(1)求数列{an}的通项公式；
(2)对任意m∈N*，将数列{an}中落入区间(9m,92m)内的项的个数记为bm，求数列{bm}的前m项和Sm.
(1)求数列{an}的通项公式；
(2)对任意m∈N*，将数列{an}中落入区间(9m,92m)内的项的个数记为bm，求数列{bm}的前m项和Sm.
（1）9n－8(n∈N*)．（2）
(1)因为{an}是一个等差数列，
所以a3＋a4＋a5＝3a4＝84，所以a4＝28.
设数列{an}的公差为d，
则5d＝a9－a4＝73－28＝45，故d＝9.
由a4＝a1＋3d得28＝a1＋3×9，即a1＝1，
所以an＝a1＋(n－1)d＝1＋9(n－1)＝9n－8(n∈N*)．
(2)对m∈N*，若9m＜an＜92m，
则9m＋8＜9n＜92m＋8，
因此9m－1＋1≤n≤92m－1，
故得bm＝92m－1－9m－1.
于是Sm＝b1＋b2＋b3＋…＋bm＝(9＋93＋…＋92m－1)－(1＋9＋…＋9m－1)
＝
.
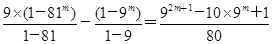所以a3＋a4＋a5＝3a4＝84，所以a4＝28.
设数列{an}的公差为d，
则5d＝a9－a4＝73－28＝45，故d＝9.
由a4＝a1＋3d得28＝a1＋3×9，即a1＝1，
所以an＝a1＋(n－1)d＝1＋9(n－1)＝9n－8(n∈N*)．
(2)对m∈N*，若9m＜an＜92m，
则9m＋8＜9n＜92m＋8，
因此9m－1＋1≤n≤92m－1，
故得bm＝92m－1－9m－1.
于是Sm＝b1＋b2＋b3＋…＋bm＝(9＋93＋…＋92m－1)－(1＋9＋…＋9m－1)
＝
.
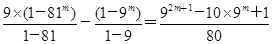练习册系列答案
相关题目
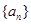满足：
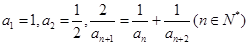，则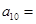
__________.