题目内容
如图是见证魔术师“论证”64=65飞神奇.对这个乍看起来颇为神秘的现象,我们运用数学知识不难发现其中的谬误.另外,我们可以更换图中的数据,就能构造出许多更加直观与“令人信服”的“论证”.
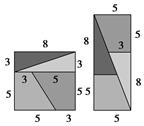
请你用数列知识归纳:(1)这些图中的数所构成的数列:________;(2)写出与这个魔术关联的一个数列递推关系式:________.

请你用数列知识归纳:(1)这些图中的数所构成的数列:________;(2)写出与这个魔术关联的一个数列递推关系式:________.
(1)an+2=an+1+an,a1=1,a2=1
(2)an+2·an-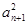 =(-1)n-1和
=(-1)n-1和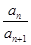 ≈0.618.
≈0.618.
(2)an+2·an-
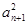 =(-1)n-1和
=(-1)n-1和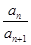 ≈0.618.
≈0.618.利用推理知识求解.由图形可知,图中的数构成裴波纳契数列,所以(1)an+2=an+1+an,a1=1,a2=1;(2)题右图中间实质上有一个面积是1的平行四边形,有时空着,有时重合,所以与魔术有关的数列递推关系式可能是an+2·an-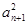 =(-1)n-1和
=(-1)n-1和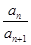 ≈0.618.
≈0.618.
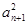 =(-1)n-1和
=(-1)n-1和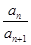 ≈0.618.
≈0.618.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
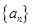 的前n项和
的前n项和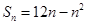
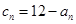 ,求数列
,求数列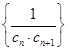 的前
的前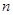 项和
项和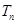
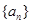 (n
(n )的公差为3,从
)的公差为3,从 是等差数列,若
是等差数列,若 则数列
则数列