题目内容
【题目】给定常数c＞0，定义函数f（x）=2|x+c+4|﹣|x+c|．数列a1 ， a2 ， a3 ， …满足an+1=f（an），n∈N* ．
（1）若a1=﹣c﹣2，求a2及a3；
（2）求证：对任意n∈N* ， an+1﹣an≥c；
（3）是否存在a1 ， 使得a1 ， a2 ， …，an ， …成等差数列？若存在，求出所有这样的a1；若不存在，说明理由．
【答案】
（1）
解：a2=f（a1）=f（﹣c﹣2）=2|﹣c﹣2+c+4|﹣|﹣c﹣2+c|=4﹣2=2，
a3=f（a2）=f（2）=2|2+c+4|﹣|2+c|=2（6+c）﹣（c+2）=10+c．
（2）
证明：由已知可得f（x）=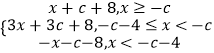 
当an≥﹣c时，an+1﹣an=c+8＞c；
当﹣c﹣4≤an＜﹣c时，an+1﹣an=2an+3c+8≥2（﹣c﹣4）+3c+8=c；
当an＜﹣c﹣4时，an+1﹣an=﹣2an﹣c﹣8＞﹣2（﹣c﹣4）﹣c﹣8=c．
∴对任意n∈N*，an+1﹣an≥c；
（3）
解：假设存在a1，使得a1，a2，…，an，…成等差数列．
由（2）及c＞0，得an+1≥an，即{an}为无穷递增数列．
又{an}为等差数列，所以存在正数M，当n＞M时，an≥﹣c，从而an+1=f（an）=an+c+8，由于{an}为等差数列，
因此公差d=c+8．
①当a1＜﹣c﹣4时，则a2=f（a1）=﹣a1﹣c﹣8，
又a2=a1+d=a1+c+8，故﹣a1﹣c﹣8=a1+c+8，即a1=﹣c﹣8，从而a2=0，
当n≥2时，由于{an}为递增数列，故an≥a2=0＞﹣c，
∴an+1=f（an）=an+c+8，而a2=a1+c+8，故当a1=﹣c﹣8时，{an}为无穷等差数列，符合要求；
②若﹣c﹣4≤a1＜﹣c，则a2=f（a1）=3a1+3c+8，又a2=a1+d=a1+c+8，∴3a1+3c+8=a1+c+8，得a1=﹣c，应舍去；
③若a1≥﹣c，则由an≥a1得到an+1=f（an）=an+c+8，从而{an}为无穷等差数列，符合要求．
综上可知：a1的取值范围为{﹣c﹣8}∪[﹣c，+∞）．
【解析】（1）对于分别取n=1，2，an+1=f（an），n∈N* ． 去掉绝对值符合即可得出；（2）由已知可得f（x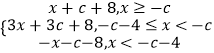）= ，分三种情况讨论即可证明；（3）由（2）及c＞0，得an+1≥an ， 即{an}为无穷递增数列．分以下三种情况讨论：当a1＜﹣c﹣4时，当﹣c﹣4≤a1＜﹣c时，当a1≥﹣c时．即可得出a1的取值范围．
【考点精析】本题主要考查了等差关系的确定的相关知识点，需要掌握如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，即
－
=d ，（n≥2，n∈N
）那么这个数列就叫做等差数列才能正确解答此题．
