题目内容
4．椭圆中心在原点，对称轴为坐标轴，离心率为$\frac{1}{2}$，长轴长为8，求该椭圆标准方程．分析 依题意，e=$\frac{c}{a}$=$\frac{1}{2}$，a=4，求出b，分焦点在x轴与焦点在y轴讨论即可求得答案．
解答 解：依题意，e=$\frac{c}{a}$=$\frac{1}{2}$，a=4，
∴c=2，b2=a2-c2=16-4=12，
∴当焦点在x轴时，椭圆的标准方程为$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}$=1；
当焦点在y轴时，椭圆的标准方程为$\frac{{y}^{2}}{16}+\frac{{x}^{2}}{12}$=1．
点评 本题考查椭圆的简单性质，考查分类讨论思想与运算能力，属于中档题．
练习册系列答案
相关题目
如图，在△ABC中，已知点D在BC边上，AD•sin∠C+AC•sin∠ADC=DC•sin∠DAC，sin∠BAC=$\frac{2\sqrt{2}}{3}$，AB=3$\sqrt{2}$，AD=3．
12．已知函数f（x）=e|x|+x2，则使得f（x）＞f（2x-1）成立的x的取值范围是（ ）
| A． | $（{\frac{1}{3}，1}）$ | B． | $（{-∞，\frac{1}{3}}）∪（{1，+∞}）$ | C． | （-$\frac{1}{3}$，$\frac{1}{3}$） | D． | $（{-∞，-\frac{1}{3}}）∪（{\frac{1}{3}，+∞}）$ |
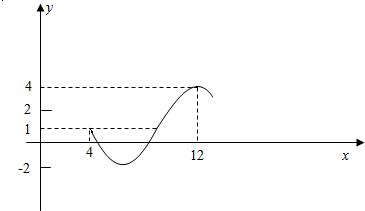如图为函数y=Asin（ωx+ϕ）+c（A＞0，ω＞0，ϕ＞0）图象的一部分，求此函数的解析式．