题目内容
【题目】平面直角坐标系xOy中，A（2，4），B（﹣1，2），C，D为动点，
（1）若C（3，1），求平行四边形ABCD的两条对角线的长度
（2）若C（a，b），且 
，求 
取得最小值时a，b的值．
【答案】
（1）解： 
=（1，﹣3）， 
=（3，2）．
= 
= 
．
由平行四边形的性质可得： 
= ，可得 
= 
+ =（6，3）．
∴ 
=（7，1），可得： 
= 
=5 
（2）解：C（a，b），且 
，∴ = +（3，1）=（a+3，b+1）．
∴ =（a+4，b﹣1）．
=（a﹣2，b﹣4）．
∴ 
=（a﹣2）（a+4）+（b﹣4）（b﹣1）=a2+2a﹣8+b2﹣5b+4
=（a+1）2+ 
﹣ 
≥ 
，当且仅当a=﹣1，b= 
时取等号
【解析】（1） =（1，﹣3）， =（3，2）．可得 ．由平行四边形的性质可得： = ，可得 = + ．可得 ．（2）C（a，b），且 ，可得 = +（3，1），可得 =（a+4，b﹣1）． =（a﹣2，b﹣4）．利用数量积运算性质、二次函数的单调性即可得出．
【题目】“奶茶妹妹”对某时间段的奶茶销售量及其价格进行调查，统计出售价x元和销售量y杯之间的一组数据如下表所示：
价格x | 5 | 5.5 | 6.5 | 7 |
销售量y | 12 | 10 | 6 | 4 |
通过分析，发现销售量y对奶茶的价格x具有线性相关关系．
（Ⅰ）求销售量y对奶茶的价格x的回归直线方程；
（Ⅱ）欲使销售量为13杯，则价格应定为多少？
注：在回归直线y= 
中， 
， 
= 
﹣ 
． 
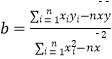=146.5．
【题目】为考察高中生的性别与是否喜欢数学课程之间的关系，在某城市的某校高中生中，从男生中随机抽取了70人，从女生中随机抽取了50人，男生中喜欢数学课程的占
，女生中喜欢数学课程的占
，得到如下列联表.
喜欢数学课程 | 不喜欢数学课程 | 合计 | ||||||||
男生 | ||||||||||
女生 | ||||||||||
合计 | ||||||||||
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 | |||
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 | |||
（1）请将列联表补充完整；试判断能否有90%的把握认为喜欢数学课程与否与性别有关；
（2）从不喜欢数学课程的学生中采用分层抽样的方法，随机抽取6人，现从6人中随机抽取2人，若所选2名学生中的女生人数为
，求的分布列及数学期望.
附：
，其中
.
