题目内容
(本小题满分13分)
设函数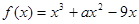 的导函数为
的导函数为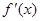 ,且
,且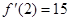 。
。
(Ⅰ)求函数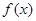 的图象在x=0处的切线方程;
的图象在x=0处的切线方程;
(Ⅱ)求函数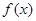 的极值。
的极值。
设函数
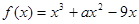 的导函数为
的导函数为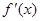 ,且
,且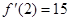 。
。(Ⅰ)求函数
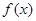 的图象在x=0处的切线方程;
的图象在x=0处的切线方程;(Ⅱ)求函数
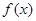 的极值。
的极值。(Ⅰ)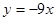 (Ⅱ)当x=-3时,
(Ⅱ)当x=-3时,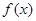 有极大值27;当x=1时,
有极大值27;当x=1时,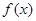 有极小值-5
有极小值-5
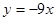 (Ⅱ)当x=-3时,
(Ⅱ)当x=-3时,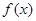 有极大值27;当x=1时,
有极大值27;当x=1时,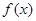 有极小值-5
有极小值-5试题分析:(Ⅰ)因为
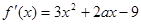 , 1分
, 1分所以由
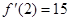 ,得a=3, 3分
,得a=3, 3分则
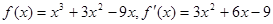 。
。所以
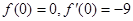 , 4分
, 4分所以函数
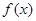 的图象在x=0处的切线方程为
的图象在x=0处的切线方程为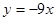 。 6分
。 6分(Ⅱ)令
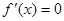 ,得x=-3或x=1。 7分
,得x=-3或x=1。 7分当x变化时,
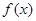 与
与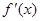 的变化情况如下表:
的变化情况如下表:| x | (-∞,-3) | -3 | (-3,1) | 1 | (1,+∞) |
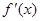 | + | 0 | - | 0 | + |
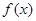 | ↗ | 27 | ↘ | -5 | ↗ |
即函数
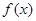 在(-∞,-3)上单调递增,在(-3,1)上单调递减,在(1,+∞)上单调递增。
在(-∞,-3)上单调递增,在(-3,1)上单调递减,在(1,+∞)上单调递增。所以当x=-3时,
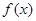 有极大值27;当x=1时,
有极大值27;当x=1时,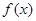 有极小值-5。 13分
有极小值-5。 13分点评:函数在某点处的导数等于该点处的切线斜率,求函数极值先要通过导数求的极值点及单调区间,从而确定是极大值还是极小值

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
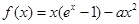
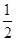 ,求f(x)的单调区间;
,求f(x)的单调区间;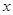 ≥0时f(x)≥0,求a的取值范围。
≥0时f(x)≥0,求a的取值范围。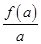 ,
, 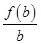 ,
,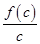 的大小关系是
的大小关系是 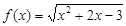 的递减区间是 。
的递减区间是 。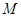 是由满足下述条件的函数构成的集合:对任意
是由满足下述条件的函数构成的集合:对任意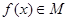 ,
,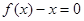 有实数根;② 函数
有实数根;② 函数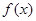 的导数
的导数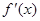 满足
满足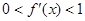 .
.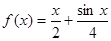 是否是集合
是否是集合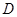 ,则对于任意
,则对于任意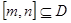 ,都存在
,都存在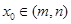 ,使得等式
,使得等式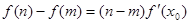 成立.试用这一性质证明:方程
成立.试用这一性质证明:方程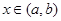 ,求证:对于
,求证:对于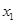 ,
,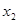 ,
,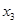 ,当
,当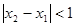 ,且
,且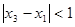 时,
时,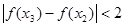
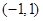 上的函数
上的函数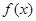 满足:对任意
满足:对任意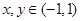 ,
,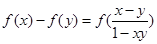 恒成立.有下列结论:①
恒成立.有下列结论:①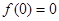 ;②函数
;②函数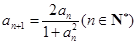 ,且
,且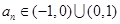 ,则数列
,则数列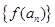 为等比数列.
为等比数列.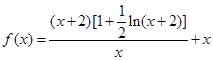
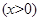
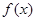 在
在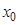 处取得极值,且
处取得极值,且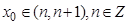 ,求
,求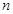 的值,并说明
的值,并说明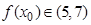
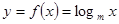 ,
,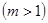 在
在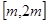 上的最大值是最小值的2倍,
上的最大值是最小值的2倍,