题目内容
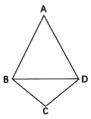
【题目】如图,四边形![]() ,
,![]() ,
,![]() ,现将
,现将![]() 沿
沿![]() 折起,当二面角
折起,当二面角![]() 的大小在
的大小在![]() 时,直线
时,直线![]() 和
和![]() 所成角为
所成角为![]() ,则
,则![]() 的最大值为( )
的最大值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
取BD中点O,连结AO,CO,以O为原点,OC为x轴,OD为y轴,过点O作平面BCD的垂线为z轴,建立空间直角坐标系,利用向量法能求出直线AB与CD所成角的余弦值取值范围.
解:取BD中点O,连结AO,CO,
∵AB=BD=DA=4.BC=CD![]() ,∴CO⊥BD,AO⊥BD,且CO=2,AO
,∴CO⊥BD,AO⊥BD,且CO=2,AO![]() ,
,
∴∠AOC是二面角A﹣BD﹣C的平面角,
以O为原点,OC为x轴,OD为y轴,
过点O作平面BCD的垂线为z轴,建立空间直角坐标系,
B(0,﹣2,0),C(2,0,0),D(0,2,0),
设二面角A﹣BD﹣C的平面角为θ,则![]() ,
,
连AO、BO,则∠AOC=θ,A(![]() ),
),
∴![]() ,
,![]() ,
,
设AB、CD的夹角为α,
则cosα ,
,
∵![]() ,∴cos
,∴cos![]() ,∴|1
,∴|1![]() |∈[0,1+
|∈[0,1+![]() ].
].
∴cos![]() 的最大值为
的最大值为![]() .
.
故选:C.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目






