题目内容
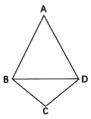
【题目】如图1,在长方形![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 为线段
为线段![]() 上一动点.现将
上一动点.现将![]() 沿
沿![]() 折起,形成四棱锥
折起,形成四棱锥![]() .
.

(1)若![]() 与
与![]() 重合,且
重合,且![]() (如图2).证明:
(如图2).证明:![]() 平面
平面![]() ;
;
(2)若![]() 不与
不与![]() 重合,且平面
重合,且平面![]() 平面
平面![]() (如图3),设
(如图3),设![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析;
(2)![]() .
.
【解析】
(1)由AD⊥BD,AD⊥DE,BD∩DE=D,可得AD⊥平面BDE,可得AD⊥BE.由E与O重合,可得△ADE与△BCE都为等腰直角三角形,可得BE⊥AE.即可证明结论.
(2)过E点作EH⊥AB,垂足为H,并连接DH,证明EH⊥DH,设CE=x,则DE=4﹣x,在Rt△DHB中列出t关于x的函数关系式,利用二次函数求最值即可
(1)由![]() 与
与![]() 重合,则有
重合,则有![]() , 因为AD⊥BD,
, 因为AD⊥BD,![]() ,所以
,所以![]() 平面
平面![]() ,
,![]() ,
,
![]() ,所以
,所以![]() 平面
平面![]() .
.


(2)如图过E点作EH⊥AB,垂足为H,并连接DH,
又∵平面ABD⊥平面ABC,平面ABD∩平面ABC=AB,EH平面ABC,
∴EH⊥平面ABD,∵DH平面ABD,∴EH⊥DH,
设CE=x,则DE=4﹣x,
∵BC⊥AB,∴BC∥EH,又CE∥AB,∴BH=x,EH=2,
∴在Rt△DHE中,DH![]() ,
,
∴在Rt△DHB中,t![]() ,
,
∵x∈[0,2),∴t∈![]() .
.


 学习实践园地系列答案
学习实践园地系列答案【题目】利用独立性检验的方法调查高中生性别与爱好某项运动是否有关,通过随机调查200名高中生是否爱好某项运动,利用![]() 列联表,由计算可得
列联表,由计算可得![]() ,参照下表:
,参照下表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5,024 | 6.635 | 7.879 | 10.828 |
得到的正确结论是( )
A. 有99%以上的把握认为“爱好该项运动与性别无关”
B. 有99%以上的把握认为“爱好该项运动与性别有关”
C. 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别无关”