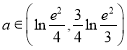Question

【题目】已双曲线的一条渐近线与椭圆C：（）在第一象限的交点为P，，为椭圆C的左、右焦点，若，则椭圆C的离心率为（ ）

A.B.C.D.

Answer 1

【答案】A

【解析】

求得双曲线的渐近线方程，联立椭圆方程，求得P的坐标，设|PF1|=m，|PF2|=n，运用椭圆的定义和三角形的余弦定理和面积公式可得,又，结合a，b，c的关系和离心率公式可得所求值.

设双曲线的一条渐近线方程为，

代入椭圆方程可得，

设|PF1|=m，|PF2|=n，可得m+n=2a，

由余弦定理可得（2c）2=m2+n2-2mncos60°，

化为（m+n）2-2mn-mn=4c2，即为mn=

则,

又,

可得，结合b2=a2-c2，

化为7a4-22c2a2+3c4=0，

可得a2=3c2或c2=7a2（舍去），

则e=,

故选：A．