题目内容
【题目】设![]() 为数列
为数列![]() 的前
的前![]() 项和,若
项和,若![]() (
(![]() 为常数)对任意
为常数)对任意![]() 恒成立.
恒成立.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,且
,且![]() .
.
①求数列![]() 的通项公式;
的通项公式;
②若数列![]() 满足
满足![]() ,且
,且![]() ,求证:数列
,求证:数列![]() 为等比数列.
为等比数列.
【答案】(1)![]() ;(2)①
;(2)①![]() ,②证明见解析.
,②证明见解析.
【解析】
(1)由题可得数列![]() 为等比数列,则可得
为等比数列,则可得![]() ,进而答案可求;
,进而答案可求;
(2)①![]() ,利用
,利用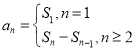 求数列
求数列![]() 的通项公式;
的通项公式;
②由①可得![]() ,则
,则![]() ,又
,又![]() ,可求出
,可求出![]() ,
,![]() ,计算
,计算![]() ,进一步
,进一步![]() ,则可得
,则可得![]() ,代入
,代入![]() 计算可得
计算可得![]() ,得证.
,得证.
(1)因为![]() ,所以
,所以![]() ,所以数列
,所以数列![]() 为等比数列.
为等比数列.
所以![]() ,所以
,所以![]() .
.
(2)①![]() .
.
当![]() 时,
时,![]() ,解得
,解得![]() 或
或![]() (舍去).
(舍去).
当![]() 时,
时,![]() ,
,
化简得:![]() .
.
又因为![]() ,所以
,所以![]() ,所以数列
,所以数列![]() 为等差数列,所以
为等差数列,所以![]() .
.
②因为![]() ,所以当
,所以当![]() 时,
时,![]() .
.
又因为![]() ,所以
,所以![]() .
.
当![]() 时,
时,![]() ,解得
,解得![]() .
.
因为![]() ,所以
,所以![]() ,两式相除得,
,两式相除得,![]() .
.
因为![]() ,所以
,所以![]() ,两式相除得,
,两式相除得,![]() ,
,
所以![]() .
.
又因为![]() ,所以
,所以![]() ,即
,即![]() .
.
所以数列![]() 为等比数列.
为等比数列.

练习册系列答案
相关题目