题目内容
11.已知矩阵A=$[\begin{array}{l}{1}&{0}\\{1}&{1}\end{array}]$,B=$[\begin{array}{l}{0}&{2}\\{3}&{2}\end{array}]$.(1)求满足条件AM=B的矩阵M;
(2)矩阵M对应的变换将曲线C:x2+y2=1变换为曲线C′,求曲线C′的方程.
分析 (1)利用待定系数法,求满足条件AM=B的矩阵M;
(2)建立曲线C上任意一点P(x,y)在矩阵M对应的变换作用下变为点P′(x′,y′)的关系,将点P(x,y)的坐标代入圆的方程即可求出.
解答 解:(1)设M=$[\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}]$,
AM=$[\begin{array}{l}{1}&{0}\\{1}&{1}\end{array}]$$[\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}]$=$[\begin{array}{l}{a}&{b}\\{a+c}&{b+d}\end{array}]$=$[\begin{array}{l}{0}&{2}\\{3}&{2}\end{array}]$,
得a=0,b=2,c=3,d=0.
∴M=$[\begin{array}{l}{0}&{2}\\{3}&{0}\end{array}]$.
(2)设曲线C上任意一点P(x,y)在矩阵M对应的变换作用下变为点P′(x′,y′),
则M$[\begin{array}{l}{x}\\{y}\end{array}]$=$[\begin{array}{l}{0}&{2}\\{3}&{2}\end{array}]$$[\begin{array}{l}{x}\\{y}\end{array}]$=$[\begin{array}{l}{2y}\\{3x}\end{array}]$=$[\begin{array}{l}{x′}\\{y′}\end{array}]$,
∴2y=x′,3x=y′
即y=$\frac{x′}{2}$,x=$\frac{y′}{3}$
代入曲线C:x2+y2=1,得($\frac{x′}{2}$)2+($\frac{y′}{3}$)2=1.
∴曲线C′的方程是$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{9}$=1.
点评 本题主要考查矩阵与变换、曲线在矩阵变换下的曲线的方程,考查运算求解能力及化归与转化思想.

| A. | $\sqrt{5}$ | B. | $\frac{{\sqrt{7}}}{2}$ | C. | $\sqrt{7}$ | D. | $\frac{{\sqrt{21}}}{3}$ |
 如图,圆锥的顶点为P,底面圆为O,底面的一条直径为AB,C为半圆弧$\widehat{AB}$的中点,E为劣弧$\widehat{CB}$的中点,已知PO=2,OA=1,求三棱锥P-AOC的体积,并求异面直线PA和OE所成角的大小.
如图,圆锥的顶点为P,底面圆为O,底面的一条直径为AB,C为半圆弧$\widehat{AB}$的中点,E为劣弧$\widehat{CB}$的中点,已知PO=2,OA=1,求三棱锥P-AOC的体积,并求异面直线PA和OE所成角的大小. 中,
中, ,过
,过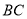 的中点
的中点 作平面
作平面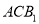 的垂线,交平面
的垂线,交平面 于
于 ,则
,则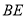 与平面
与平面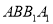 所成角的正切值为( )
所成角的正切值为( )
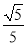 B.
B.
 D.
D.