题目内容
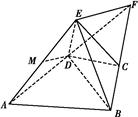
如图,几何体E ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
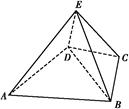
(1)求证:BE=DE;
(2)若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.
 ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
(1)求证:BE=DE;
(2)若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.
(1)见解析 (2)见解析
证明:(1)如图所示,取BD的中点O,连接CO,EO.
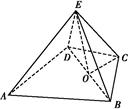
由于CB=CD,
所以CO⊥BD.
又EC⊥BD,EC∩CO=C,
CO,EC?平面EOC,
所以BD⊥平面EOC,
因此BD⊥EO.
又O为BD的中点,
所以BE=DE.
(2)法一 如图所示,取AB的中点N,连接DM,DN,MN.
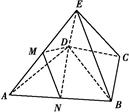
因为M是AE的中点,
所以MN∥BE.
又MN
 平面BEC,
平面BEC,BE?平面BEC,
所以MN∥平面BEC.
又因为△ABD为正三角形,
所以∠BDN=30°.
又CB=CD,∠BCD=120°,
因此∠CBD=30°.
所以DN∥BC.
又DN
 平面BEC,BC?平面BEC,
平面BEC,BC?平面BEC,所以DN∥平面BEC.
又MN∩DN=N,
所以平面DMN∥平面BEC.
又DM?平面DMN,
所以DM∥平面BEC.
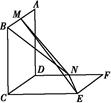
法二 如图所示,延长AD,BC交于点F,连接EF.
因为CB=CD,∠BCD=120°,
所以∠CBD=30°.
因为△ABD为正三角形,
所以∠BAD=60°,
∠ABC=90°,
因此∠AFB=30°,
所以AB=
 AF.
AF.又AB=AD,
所以D为线段AF的中点,
连接DM,由点M是线段AE的中点,
得DM∥EF.
又DM
 平面BEC,EF?平面BEC,
平面BEC,EF?平面BEC,所以DM∥平面BEC.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
 中,底面
中,底面 为平行四边形,
为平行四边形, ,
, ,
,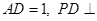 底面
底面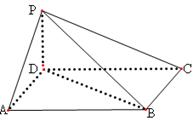
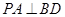 ;
;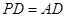 ,求二面角
,求二面角 余弦值.
余弦值.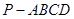 中,
中,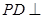 平面
平面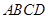 ,底面
,底面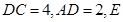 为
为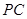 的中点.
的中点.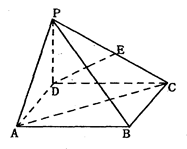
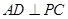 ;
;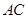 上是否存在一点
上是否存在一点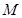 ,使得
,使得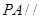 平面
平面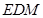 ?若存在,求出
?若存在,求出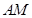 的长;若不存在,请说明理由.
的长;若不存在,请说明理由. A1B1C1,
A1B1C1,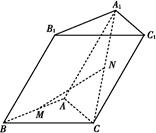
 沿对角线
沿对角线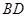 折成直二面角
折成直二面角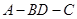 ,有如下四个结论:
,有如下四个结论: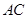 ⊥
⊥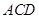 是等边三角形;③
是等边三角形;③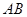 与平面
与平面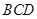 所成的角为60°;
所成的角为60°;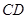 所成的角为60°.其中错误的结论是
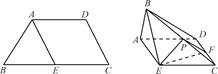
所成的角为60°.其中错误的结论是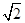 ,将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中,下列说法正确的是________.(填序号)
,将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中,下列说法正确的是________.(填序号)