题目内容
12.设a、b都是不等于1的正数,则“3a>3b>3”是“loga3<logb3”的( )| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
分析 求解3a>3b>3,得出a>b>1,
loga3<logb3,$\left\{\begin{array}{l}{lgb-lga<0}\\{lgalgb>0}\end{array}\right.$或$\left\{\begin{array}{l}{lgb-lga>0}\\{lgalgb<0}\end{array}\right.$根据对数函数的性质求解即可,
再利用充分必要条件的定义判断即可.
解答 解:a、b都是不等于1的正数,
∵3a>3b>3,
∴a>b>1,
∵loga3<logb3,
∴$\frac{1}{lga}$$<\frac{1}{lgb}$,
即$\frac{lgb-lga}{lgalgb}$<0,
$\left\{\begin{array}{l}{lgb-lga<0}\\{lgalgb>0}\end{array}\right.$或$\left\{\begin{array}{l}{lgb-lga>0}\\{lgalgb<0}\end{array}\right.$
求解得出:a>b>1或1>a>b>0或b>1,0<a<1
根据充分必要条件定义得出:“3a>3b>3”是“loga3<logb3”的充分条不必要件,
故选:B.
点评 本题综合考查了指数,对数函数的单调性,充分必要条件的定义,属于综合题目,关键是分类讨论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.如图所示程序框图,则满足|x|+|y|≤2的输出的有序实数对(x,y)的概率为( )


| A. | $\frac{1}{16}$ | B. | $\frac{3}{32}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
20.已知x,y满足约束条件$\left\{\begin{array}{l}{x-y≥0}\\{x+y≤2}\\{y≥0}\end{array}\right.$,若z=ax+y的最大值为4,则a=( )
| A. | 3 | B. | 2 | C. | -2 | D. | -3 |
7.设i是虚数单位,则复数i3-$\frac{2}{i}$=( )
| A. | -i | B. | -3i | C. | i | D. | 3i |
2.将函数f(x)=sin2x的图象向右平移φ(0<φ<$\frac{π}{2}$)个单位后得到函数g(x)的图象.若对满足|f(x1)-g(x2)|=2的x1、x2,有|x1-x2|min=$\frac{π}{3}$,则φ=( )
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
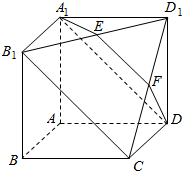 如图所示,在多面体A1B1D1DCBA中,四边形AA1B1B,ADD1A1,ABCD均为正方形,E为B1D1的中点,过A1,D,E的平面交CD1于F.
如图所示,在多面体A1B1D1DCBA中,四边形AA1B1B,ADD1A1,ABCD均为正方形,E为B1D1的中点,过A1,D,E的平面交CD1于F. 如图,AB为圆O的直径,E为AB 的延长线上一点,过E作圆O的切线,切点为C,过A作直线EC的垂线,垂足为D.若AB=4.CE=2$\sqrt{3}$,则 AD=3.
如图,AB为圆O的直径,E为AB 的延长线上一点,过E作圆O的切线,切点为C,过A作直线EC的垂线,垂足为D.若AB=4.CE=2$\sqrt{3}$,则 AD=3.