题目内容
8.若函数f(x)=$\frac{{2}^{x}+1}{{2}^{x}-a}$是奇函数,则使f(x)>3成立的x的取值范围为( )| A. | (-∞,-1) | B. | (-1,0) | C. | (0,1) | D. | (1,+∞) |
分析 由f(x)为奇函数,根据奇函数的定义可求a,代入即可求解不等式.
解答 解:∵f(x)=$\frac{{2}^{x}+1}{{2}^{x}-a}$是奇函数,
∴f(-x)=-f(x)
即$\frac{{2}^{-x}+1}{{2}^{-x}-a}=\frac{{2}^{x}+1}{a-{2}^{x}}$
整理可得,$\frac{1+{2}^{x}}{1-a•{2}^{x}}=\frac{1+{2}^{x}}{a-{2}^{x}}$
∴1-a•2x=a-2x
∴a=1,
∴f(x)=$\frac{{2}^{x}+1}{{2}^{x}-1}$
∵f(x))=$\frac{{2}^{x}+1}{{2}^{x}-1}$>3
∴$\frac{{2}^{x}+1}{{2}^{x}-1}$-3=$\frac{4-2•{2}^{x}}{{2}^{x}-1}$>0,
整理可得,$\frac{{2}^{x}-2}{{2}^{x}-1}<0$,
∴1<2x<2
解可得,0<x<1
故选:C
点评 本题主要考查了奇函数的定义的应用及分式不等式的求解,属于基础试题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
18.已知$\overrightarrow{a}$是以点A(3,-1)为起点,且与$\overrightarrow{b}$=(-3,4)平行的单位向量,则$\overrightarrow{a}$的终点坐标是( )
| A. | ($\frac{3}{5}$,-$\frac{4}{5}$)或(-$\frac{3}{5}$,$\frac{4}{5}$) | B. | ($\frac{5}{13}$,-$\frac{12}{13}$)或(-$\frac{5}{13}$,$\frac{12}{13}$) | ||
| C. | ($\frac{12}{5}$,-$\frac{1}{5}$)或($\frac{18}{5}$,-$\frac{9}{5}$) | D. | ($\frac{12}{5}$,$\frac{1}{5}$)或($\frac{18}{5}$,$\frac{9}{5}$) |
16.已知m,n是两条不同直线,α,β是两个不同平面,则下列命题正确的是( )
| A. | 若α,β垂直于同一平面,则α与β平行 | |
| B. | 若m,n平行于同一平面,则m与n平行 | |
| C. | 若α,β不平行,则在α内不存在与β平行的直线 | |
| D. | 若m,n不平行,则m与n不可能垂直于同一平面 |
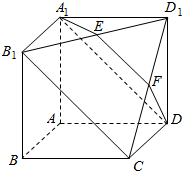 如图所示,在多面体A1B1D1DCBA中,四边形AA1B1B,ADD1A1,ABCD均为正方形,E为B1D1的中点,过A1,D,E的平面交CD1于F.
如图所示,在多面体A1B1D1DCBA中,四边形AA1B1B,ADD1A1,ABCD均为正方形,E为B1D1的中点,过A1,D,E的平面交CD1于F.