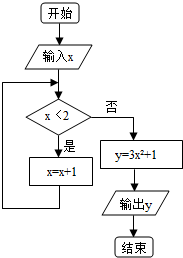
题目内容
18.△ABC是边长为2的等边三角形,已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{AB}$=2$\overrightarrow{a}$,$\overrightarrow{AC}$=2$\overrightarrow{a}$+$\overrightarrow{b}$,则下列结论正确的是( )| A. | |$\overrightarrow{b}$|=1 | B. | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | C. | $\overrightarrow{a}$•$\overrightarrow{b}$=1 | D. | (4$\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{BC}$ |
分析 由题意,知道$\overrightarrow{a}=\frac{1}{2}\overrightarrow{AB}$,$\overrightarrow{b}=\overrightarrow{BC}$,根据已知三角形为等边三角形解之.
解答 解:因为已知三角形ABC的等边三角形,$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{AB}$=2$\overrightarrow{a}$,$\overrightarrow{AC}$=2$\overrightarrow{a}$+$\overrightarrow{b}$,又$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}$,∴$\overrightarrow{b}$的方向应该为$\overrightarrow{BC}$的方向.
所以$\overrightarrow{a}=\frac{1}{2}\overrightarrow{AB}$,$\overrightarrow{b}=\overrightarrow{BC}$,
所以$|\overrightarrow{b}|$=2,$\overrightarrow{a}•\overrightarrow{b}$=1×2×cos120°=-1,
4$\overrightarrow{a}•\overrightarrow{b}$=4×1×2×cos120°=-4,${\overrightarrow{b}}^{2}$=4,所以$4\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}$=0,即(4$\overrightarrow{a}+\overrightarrow{b}$)$•\overrightarrow{b}$=0,即$(4\overrightarrow{a}+\overrightarrow{b})•\overrightarrow{BC}$=0,所以$(4\overrightarrow{a}+\overrightarrow{b})⊥\overrightarrow{BC}$;
故选D.
点评 本题考查了向量的数量积公式的运用;注意:三角形的内角与向量的夹角的关系.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案| A. | -i | B. | -3i | C. | i | D. | 3i |
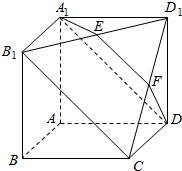 如图所示,在多面体A1B1D1DCBA中,四边形AA1B1B,ADD1A1,ABCD均为正方形,E为B1D1的中点,过A1,D,E的平面交CD1于F.
如图所示,在多面体A1B1D1DCBA中,四边形AA1B1B,ADD1A1,ABCD均为正方形,E为B1D1的中点,过A1,D,E的平面交CD1于F.