题目内容
(本小题满分12分)已知数列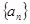 的前
的前 项和为
项和为 ,且满足
,且满足 。
。
(Ⅰ)求数列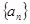 的通项公式;
的通项公式;
(Ⅱ)设 ,数列
,数列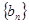 的前
的前 项和为
项和为 ,求证:
,求证: 。
。
(Ⅰ)
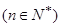 .
.
(Ⅱ)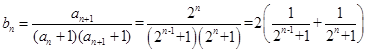 ,所以
,所以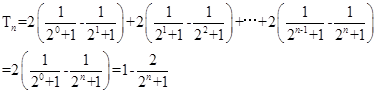
所以 。
。
解析试题分析:(Ⅰ)当 时,
时,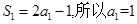 ;
;
当 时,
时,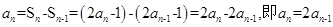 ,所以数列
,所以数列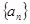 是首项为1,公比为2的等比数列。所以
是首项为1,公比为2的等比数列。所以
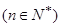 .
.
(Ⅱ)由(Ⅰ)知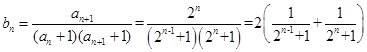 ,所以
,所以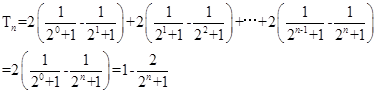
所以 。
。
考点:公式 ,
,
点评:我们要熟练掌握求数列通项公式的方法。公式法是求数列通项公式的基本方法之一,常用的公式有:等差数列的通项公式、等比数列的通项公式及公式 。此题的第一问求数列的通项公式就是用公式
。此题的第一问求数列的通项公式就是用公式 ,用此公式要注意讨论
,用此公式要注意讨论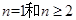 的情况。
的情况。

练习册系列答案
相关题目
已知数列{an}满足an=n·pn(n∈N+,0< p<l),下面说法正确的是( )
①当p=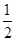 时,数列{an}为递减数列;②当
时,数列{an}为递减数列;②当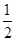 <p<l时,数列{an}不一定有最大项;
<p<l时,数列{an}不一定有最大项;
③当0<p<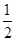 时,数列{an}为递减数列;
时,数列{an}为递减数列;
④当 为正整数时,数列{an}必有两项相等的最大项
为正整数时,数列{an}必有两项相等的最大项
| A.①② | B.③④ | C.②④ | D.②③ |
在数列 中,
中, ,且
,且 ,
, ,若数列
,若数列 满足
满足 ,则数列
,则数列 是( )
是( )
| A.递增数列 | B.递减数列 | C.常数列 | D.摆动数列 |
 满足
满足
 ,当
,当 时,求数列
时,求数列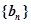 的通项公式.
的通项公式.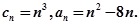 求正整数
求正整数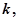 使得一切
使得一切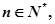 均有
均有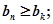
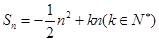 ,且Sn的最大值为8.
,且Sn的最大值为8.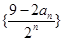 的前n项和Tn。
的前n项和Tn。 是等比数列,公比
是等比数列,公比 ,前
,前 项和为
项和为

 的通项公式;
的通项公式; 的前
的前 ,求证
,求证
 ,
,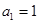 ,前
,前 项和为
项和为 .各项均为正数的等比数列列
.各项均为正数的等比数列列 满足:
满足: ,
, ,且
,且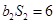 .
.
 ﹜满足:
﹜满足: .(Ⅰ)求数列﹛
.(Ⅰ)求数列﹛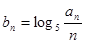 ,求
,求
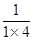 ,
,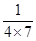 ,
,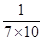 ,……,
,……, ,……
,……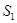 ,
,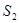 ,
,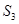 ,
,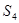
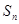 的表达式并用数学归纳法证明你的猜想。
的表达式并用数学归纳法证明你的猜想。