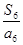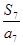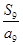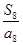题目内容
在数列 中,
中, ,且
,且 ,
, ,若数列
,若数列 满足
满足 ,则数列
,则数列 是( )
是( )
| A.递增数列 | B.递减数列 | C.常数列 | D.摆动数列 |
C
解析试题分析: ,
, 可得
可得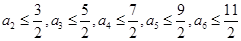 .又由
.又由 及
及 可得
可得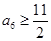 .所以
.所以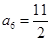 .所以由
.所以由 结合前面的式子可得.
结合前面的式子可得.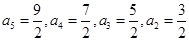 .所以在
.所以在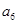 以前是一个公差为1的等差数列.同样当
以前是一个公差为1的等差数列.同样当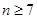 时可以得到一个公差为1的等差数列.综上
时可以得到一个公差为1的等差数列.综上 是一个首项为
是一个首项为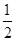 ,公差为1的等差数列
,公差为1的等差数列 .所以
.所以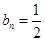 .故选C.
.故选C.
考点:1.数列的递推思想.2.等差数列的性质.3.不等式的夹击为等式的含义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
.已知数列 ,则
,则 ( )
( )
A. | B. | C.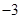 | D. |
已知
 =
= ,则
,则
 +
+
 +…+
+…+
 =( )
=( )
A. | B. | C. | D. |
设函数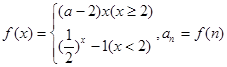 ,若数列
,若数列 是单调递减数列,则实数a的取值范围为( )
是单调递减数列,则实数a的取值范围为( )
A.(- ,2) ,2) | B.(- , , |
C.(- , , ) ) | D. |
已知数列 ,
, ,2
,2 ,
, ,…,则2
,…,则2 在这个数列中的项数为( )
在这个数列中的项数为( )
| A.6 | B.7 | C.19 | D.11 |
设an= sin
sin ,
, ,在
,在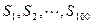 中,正数的个数是( )
中,正数的个数是( )
| A.25 |
| B.50 |
| C.75 |
| D.100 |
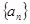 的前
的前 项和为
项和为 ,且满足
,且满足 。
。 ,数列
,数列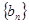 的前
的前 ,求证:
,求证: 。
。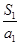 ,
,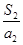 ,…,
,…,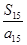 中最大的项为( )
中最大的项为( )