题目内容
已知函数f（x）=x2+bx+c的图象与x轴相切于点（3，0），函数g（x）=-2x+6，则这两个函数图象围成的区域面积为（ ）
A．
| B．
| C．2 | D．
|
∵函数f（x）=x2+bx+c的图象与x轴相切于点（3，0），
∴f′（3）=6+b=0解得b=-6
则f（x）=x2-6x+c，而点（3，0）在函数图象上
∴f（3）=9-18+c=0解得c=9
∴f（x）=x2-6x+9
联立f（x）=x2-6x+9与g（x）=-2x+6即x2-6x+9=-2x+6
解得x=1或3
∴这两个函数图象围成的区域面积为
(-2x+6-x2+6x-9)
=
(-x2+4x-3)=（-
x3+2x2-3x）
=
故选B．
∴f′（3）=6+b=0解得b=-6
则f（x）=x2-6x+c，而点（3，0）在函数图象上
∴f（3）=9-18+c=0解得c=9
∴f（x）=x2-6x+9
联立f（x）=x2-6x+9与g（x）=-2x+6即x2-6x+9=-2x+6
解得x=1或3
∴这两个函数图象围成的区域面积为
| ∫ | 31 |
=
| ∫ | 31 |
| 1 |
| 3 |
| | | 31 |
| 4 |
| 3 |
故选B．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
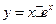的最小值为 。