题目内容
已知cosα+sinβ=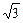
，sinα+cosβ的取值范围是D，x∈D，求函数y=
的最小值，并求取得最小值时x的值.
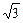，sinα+cosβ的取值范围是D，x∈D，求函数y=的最小值，并求取得最小值时x的值.
设u=sinα+cosβ
则u2+(
)2
=(sinα+cosβ)2+(cosα+sinβ)2=2+2sin(α+β)≤4.
∴u2≤1,－1≤u≤1 即D=［－1,1］,
设t=
,∵－1≤x≤1,∴1≤t≤
. x=
.
则u2+()2=(sinα+cosβ)2+(cosα+sinβ)2=2+2sin(α+β)≤4.
∴u2≤1,－1≤u≤1
即D=［－1,1］,设t=
,∵－1≤x≤1,∴1≤t≤. x=.
练习册系列答案
相关题目
的图象如下图所示．
的值； 
的图像先向_____（填“左”或“右”）平移_______个单位，
（米）是时间
（
，单位：时）的函数，记作
，下面是某日水深的数据：
．
米或
米．如果该船希望在同一天内安全进出港，请问，它至多能在港内停留多长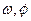
（其中
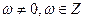）使得函数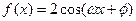
是奇函数，且在
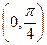上是增函数。
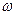与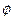
的值，并验证其符合题意；
,
，且
的取值范围；
，试求
的取小值，并求此时
的值。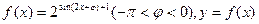
的图象的一条对称轴是直线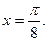
；
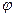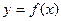的递减区间；
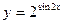的图象作怎样变换得到.
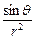，其中k是一个和灯光强度有关的常数，那么怎样选择电灯悬挂的高度h，才能使桌子边缘处最亮？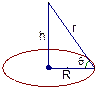
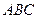中，射影定理可以表示为
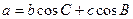，其中
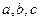分别为角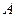
、
、
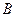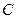的对边，类似以上定理，在四面体
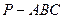中，
、
、
、
分别表示△
、△
、△
、△
，
，
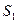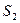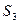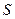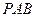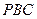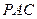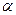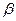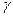分别表示面