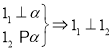题目内容
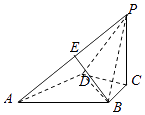
【题目】如图所示,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
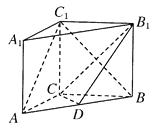
(1)求证:AC⊥BC1;
(2)求证:AC1∥平面CDB1;
(3)求异面直线AC1与B1C所成角的余弦值.
【答案】(1)见解析(2)见解析(3) ![]() .
.
【解析】试题分析:(1)由勾股定理计算得AC⊥BC,再由直棱柱性质得C1C⊥AC,最后根据线面垂直判定定理得AC⊥平面BCC1B1,即得AC⊥BC1.(2)设CB1与C1B的交点为E,由三角形中位线性质得DE∥AC1,再根据线面平行判定定理得结论(3)因为DE∥AC1,所以∠CED为AC1与B1C所成的角.再根据解三角形得所成角的余弦值.
试题解析:(1)证明:在直三棱柱ABC-A1B1C1中,底面三边长AC=3,BC=4,AB=5,∴AC⊥BC.
又∵C1C⊥AC.∴AC⊥平面BCC1B1.
∵BC1平面BCC1B,∴AC⊥BC1.
(2)证明:设CB1与C1B的交点为E,连接DE,又四边形BCC1B1为正方形.
∵D是AB的中点,E是BC1的中点,∴DE∥AC1.
∵DE平面CDB1,AC1平面CDB1,
∴AC1∥平面CDB1.
(3)∵DE∥AC1,
∴∠CED为AC1与B1C所成的角.在△CED中,ED=![]() AC1=
AC1=![]() ,
,
CD=![]() AB=
AB=![]() ,CE=
,CE=![]() CB1=2
CB1=2![]() ,∴cos∠CED=
,∴cos∠CED=![]() =
=![]() .
.
∴异面直线AC1与B1C所成角的余弦值为![]() .
.
点睛:垂直、平行关系证明中应用转化与化归思想的常见类型.
(1)证明线面、面面平行,需转化为证明线线平行.
(2)证明线面垂直,需转化为证明线线垂直.
(3)证明线线垂直,需转化为证明线面垂直.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目