题目内容
【题目】已知函数f(x)=|2x+![]() |+a|x﹣
|+a|x﹣![]() |.
|.
(Ⅰ)当a=﹣1时,解不等式f(x)≤3x;
(Ⅱ)当a=2时,若关于x的不等式2f(x)+1<|1﹣b|的解集为空集,求实数b的取值范围.
【答案】(1)![]() (2)[﹣7,9]
(2)[﹣7,9]
【解析】试题分析:
(1)零点分段可得不等式的解集为![]() ;
;
(2)利用绝对值不等式的性质,原问题转化为|1﹣b|≤8恒成立,据此可得实数b的取值范围是[﹣7,9].
试题解析:
解:(Ⅰ)当a=﹣1时,不等式f(x)=|2x+![]() |﹣|x﹣
|﹣|x﹣![]() |≤3x,
|≤3x,
等价于 ①;或
①;或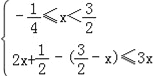 ②;或
②;或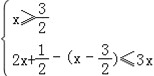 .
.
解①求得﹣![]() ≤x<﹣
≤x<﹣![]() ,解②求得﹣
,解②求得﹣![]() ≤x<
≤x<![]() ,解③求得x≥
,解③求得x≥![]() ,
,
故原不等式的解集为{x|x≥﹣![]() }.
}.
(Ⅱ)当a=2时,若关于x的不等式2f(x)+1<|1﹣b|,即 2(|2x+![]() |+2|x﹣|)+1<|1﹣b|,
|+2|x﹣|)+1<|1﹣b|,
即|4x+1|+|4x﹣6|+1<|1﹣b|.
由于|4x+1|+|4x﹣6|≥|(4x+1)﹣(4x﹣6)|=7,∴|1﹣b|>7+1的解集为,即|1﹣b|≤8恒成立,
∴﹣8≤b﹣1≤8,即﹣7≤b≤9,即要求的实数b的取值范围为[﹣7,9].

练习册系列答案
相关题目
【题目】为大力提倡“厉行节俭,反对浪费”,某高中通过随机询问100名性别不同的学生是否做到“光盘”行动,得到如表所示联表及附表:
做不到“光盘”行动 | 做到“光盘”行动 | |
男 | 45 | 10 |
女 | 30 | 15 |
P(K2≥k0) | 0.10 | 0.05 | 0.025 |
k0 | 2.706 | 3.841 | 5.024 |
经计算:K2= ![]() ≈3.03,参考附表,得到的正确结论是( )
≈3.03,参考附表,得到的正确结论是( )
A.有95%的把握认为“该学生能否做到光盘行到与性别有关”
B.有95%的把握认为“该学生能否做到光盘行到与性别无关”
C.有90%的把握认为“该学生能否做到光盘行到与性别有关”
D.有90%的把握认为“该学生能否做到光盘行到与性别无关”