题目内容
三个互不重合的平面,能把空间分成n个部分,n所有可能的值是 ( )
(A)4,6,7 (B)4,5,6,8 (C)4,7,8 (D)4,6,7,8
(A)4,6,7 (B)4,5,6,8 (C)4,7,8 (D)4,6,7,8
D
分析:将互不重合的三个平面的位置关系分为:三个平面互相平行;三个平面有两个平行,第三个平面与其它两个平面相交;三个平面交于一线;三个平面两两相交且三条交线平行;三个平面两两相交且三条交线交于一点;五种情况并分别讨论,即可得到答案.
解:若三个平面互相平行,则可将空间分为4部分;
若三个平面有两个平行,第三个平面与其它两个平面相交,则可将空间分为6部分;
若三个平面交于一线,则可将空间分为6部分;
若三个平面两两相交且三条交线平行(联想三棱柱三个侧面的关系),则可将空间分为7部分;
若三个平面两两相交且三条交线交于一点(联想墙角三个墙面的关系),则可将空间分为8部分;
故n等于4,6,7或8
故选D

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.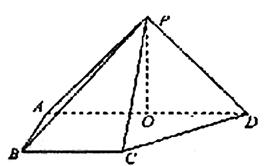
 中,指出
中,指出 ,
, 所在直线与各个面的关系.
所在直线与各个面的关系.
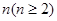 条直线,其中任意两条不平行,任意三条不共点。
条直线,其中任意两条不平行,任意三条不共点。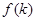 表示
表示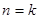 时平面被分成的区域数,则
时平面被分成的区域数,则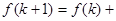 ( )
( )



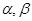 和直线,给出条件:①
和直线,给出条件:①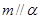 ;②
;②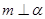 ;③
;③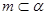 ;④
;④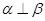 ;⑤
;⑤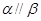 .则当满足条件 时,有
.则当满足条件 时,有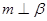 成立;(填所选条件的序号)
成立;(填所选条件的序号)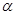 、
、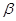 是两个不同的平面,m、n是平面
是两个不同的平面,m、n是平面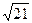
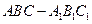 中,侧棱长为
中,侧棱长为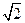 ,底面三角形的边长为1,则
,底面三角形的边长为1,则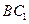 与侧面
与侧面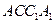 所成的角是____________
所成的角是____________