题目内容
【题目】在“挑战不可能”的电视节目上，甲、乙、丙三个人组成的解密团队参加一项解密挑战活动，规则是由密码专家给出题目，然后由3个人依次出场解密，每人限定时间是1分钟内，否则派下一个人.3个人中只要有一人解密正确，则认为该团队挑战成功，否则挑战失败.根据甲以往解密测试情况，抽取了甲100次的测试记录，绘制了如图所示的频率分布直方图.
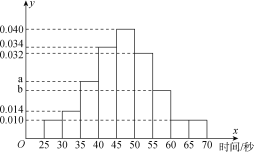
（1）若甲解密成功所需时间的中位数为47，求
、
的值，并求出甲在1分钟内解密成功的频率；
（2）在“挑战不可能”节目上由于来自各方及自身的心理压力，甲，乙，丙解密成功的概率分别为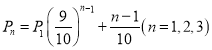
，其中
表示第
个出场选手解密成功的概率，并且
定义为甲抽样中解密成功的频率代替，各人是否解密成功相互独立.
①求该团队挑战成功的概率；
②该团队以从小到大的顺序按排甲、乙、丙三个人上场解密，求团队挑战成功所需派出的人数
的可能值及其概率.
【答案】（1）
，
，0.9；（2）①
；②1，2，3；0.009.
【解析】
(1)根据中位数为47，则在频率分布直方图中时间位于47左边的小长方形的面积之和为0.5，可求出
的值, 时间位于47右边的小长方形的面积之和为0.5，可求出
的值.
(2) ①先分别求出三人解密成功的概率，然后先求出三人都没有解密成功的概率，再求出团队解密成功的概率.
②由①可知按
从小到大的顺序的概率分别
，
，
，
的取值为1，2，3,在计算概率.
（1）甲解密成功所需时间的中位数为47，
，
解得；
，
解得；
甲在1分钟内解密成功的频率是
（2）①由题意及（1）可知第一个出场选手解密成功的概率为
；
第二个出场选手解密成功的概率为
，
第三个出场选手解密成功的概率为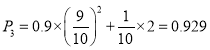
，
令“该团队挑战成功”的事件为
，“挑战不成功”的事件为
，
，
该团队挑战成功的概率为
（或该团队挑战成功的概率为
）
②由①可知按从小到大的顺序的概率分别
，
，
，
根据题意知的取值为1，2，3；
则
，
，
.
