题目内容
【题目】以下结论正确的个数是( )
①若数列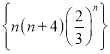 中的最大项是第
中的最大项是第![]() 项,则
项,则![]() .
.
②在![]() 中,若
中,若![]() ,则
,则![]() 为等腰直角三角形.
为等腰直角三角形.
③设![]() 、
、![]() 分别为等差数列
分别为等差数列![]() 与
与![]() 的前
的前![]() 项和,若
项和,若![]() ,则
,则![]() .
.
④![]() 的内角
的内角![]() 、
、![]() 、
、![]() 的对边分别为
的对边分别为![]() 、
、![]() 、
、![]() ,若
,若![]() 、
、![]() 、
、![]() 成等比数列,且
成等比数列,且![]() ,则
,则![]() .
.
⑤在![]() 中,
中,![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 所对边,
所对边,![]() ,则
,则![]() 的取值范围为
的取值范围为![]() .
.
A.1个B.2个C.3个D.4个
【答案】D
【解析】
对于①,由数列为正项数列可由![]() 与
与![]() ,求得
,求得![]() 的取值范围,进而判断出数列的单调性,比较端点处的项即可求得最大项; 对于②将正切化为弦,结合正弦函数的和角公式化简后即可判断三角形形状;对于③根据等差数列性质及等差数列前n项和公式,化简变形即可得解;对于④由等比中项的性质,结合余弦定理化简后即可得解;对于⑤由正弦定理,将边化为角,再根据正弦函数的图像与性质即可化简求得值域.
的取值范围,进而判断出数列的单调性,比较端点处的项即可求得最大项; 对于②将正切化为弦,结合正弦函数的和角公式化简后即可判断三角形形状;对于③根据等差数列性质及等差数列前n项和公式,化简变形即可得解;对于④由等比中项的性质,结合余弦定理化简后即可得解;对于⑤由正弦定理,将边化为角,再根据正弦函数的图像与性质即可化简求得值域.
对于①,数列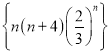 为正项数列,则
为正项数列,则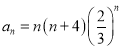 ,
,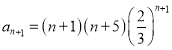 .
.
所以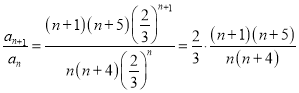 ,
,
若![]() ,即
,即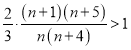 ,解得
,解得![]() ,即
,即![]() 时数列
时数列![]() 为递增数列.
为递增数列.
若![]() ,即
,即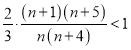 ,解得
,解得![]() ,即
,即![]() 时为递减数列.
时为递减数列.
且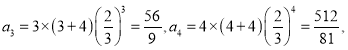 因为
因为![]() ,所以
,所以![]() 为最大项,即
为最大项,即![]() ,所以①正确.
,所以①正确.
对于②,在![]() 中,若
中,若![]() .化简可得
.化简可得![]() ,即
,即![]() ,所以
,所以![]() .两边同时乘以2,化简可得
.两边同时乘以2,化简可得![]() ,则
,则![]() 或
或![]() .即
.即![]() 或
或![]() ,所以
,所以![]() 为等腰三角形或直角三角形,故②错误;
为等腰三角形或直角三角形,故②错误;
对于③,数列![]() 与
与![]() 为等差数列,
为等差数列,![]() 、
、![]() 分别为等差数列
分别为等差数列![]() 与
与![]() 的前
的前![]() 项和.根据等差数列性质及前n项和公式可知
项和.根据等差数列性质及前n项和公式可知![]() 而
而![]() ,所以
,所以![]() ,故③正确;
,故③正确;
对于④,![]() 、
、![]() 、
、![]() 成等比数列,所以
成等比数列,所以![]() ,且
,且![]() 则
则![]() ,而
,而![]() 则由余弦定理可得
则由余弦定理可得![]() .所以④正确;
.所以④正确;
对于⑤,由正弦定理可得![]() ,
,![]() ,所以
,所以![]() .由
.由![]() 可得
可得![]() ,则
,则![]() ,
,
所以![]()
![]()
![]() ,
,
因为![]() ,
,
所以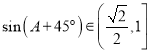 ,
,
则![]() ,
,
所以⑤正确,
综上可知,正确的有①③④⑤
故选:D

练习册系列答案
相关题目