题目内容
【题目】已知抛物线![]() 过点
过点![]() ,其焦点为
,其焦点为![]() ,且
,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)设![]() 为
为![]() 轴上异于原点的任意一点,过点
轴上异于原点的任意一点,过点![]() 作不经过原点的两条直线分别与抛物线
作不经过原点的两条直线分别与抛物线![]() 和圆
和圆![]() 相切,切点分别为
相切,切点分别为![]() ,求证:
,求证:![]() 三点共线.
三点共线.
【答案】(1)![]() (2)证明见解析
(2)证明见解析
【解析】
(1)由于![]() ,再结合抛物线
,再结合抛物线![]() 过点
过点![]() ,求解即可;
,求解即可;
(2)设![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 相切,与抛物线联立得到
相切,与抛物线联立得到![]() ,即
,即![]() ,由点
,由点![]() 关于直线
关于直线![]() 对称,得到
对称,得到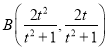 ,证明
,证明![]() ,即得证.
,即得证.
解:(1)抛物线![]() 的准线方程为
的准线方程为![]() ,
,
∴![]() .
.
又抛物线![]() 过点
过点![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴抛物线![]() 的方程为
的方程为![]() .
.
(2)证明:设![]() ,已知切线不为
,已知切线不为![]() 轴.设
轴.设![]() ,联立
,联立![]() 消去
消去![]() ,可得
,可得![]() .
.
∵直线![]() 与抛物线
与抛物线![]() 相切,
相切,
∴![]() ,即
,即![]() ,
,
代入![]() 得
得![]() ,∴
,∴![]() ,即
,即![]() .
.
设切点![]() ,则点
,则点![]() 关于直线
关于直线![]() 对称,
对称,
则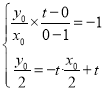 解得
解得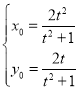 即
即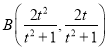 .
.
当![]() 时,直线
时,直线![]() 的斜率
的斜率![]() ,
,
直线![]() 的斜率
的斜率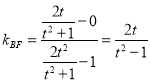 ,∴
,∴![]() ,即
,即![]() 三点共线.
三点共线.
当![]() 时,
时,![]() ,此时
,此时![]() 三点共线.
三点共线.
综上:![]() 三点共线.
三点共线.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目